Durchschnittswert
Zum Mitmachen
Nehmen Sie ein Geodreieck und einen Taschenrechner zur Hand. Drucken Sie die Seite aus und messen sie den Winkel und die Strecken in Abbildung 1 nach. Machen Sie sich die Mühe! Es lohnt sich, denn es lässt sich - nicht nur hier, sondern sehr oft - gewinnbringend einsetzen, wenn man aus einem Diagramm auf den ersten Blick Durchschnittswerte ablesen kann.
Weiter unten auf dieser Seite finden Sie ein praktisches Beispiel.
1. Wie viel Y entfällt durchschnittlich auf ein X im Punkt P?
Abbildung 1
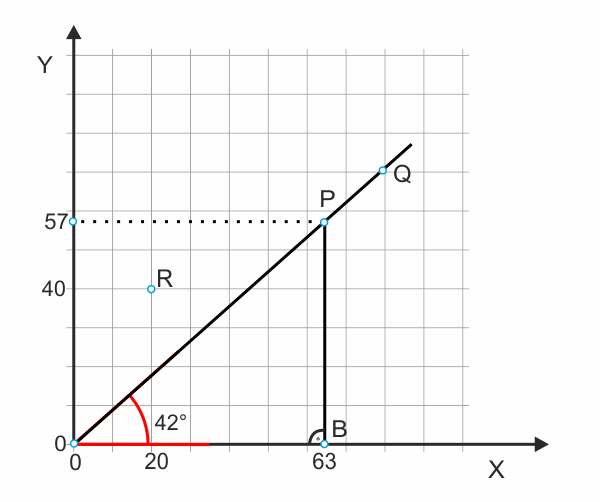
Machen Sie sich mithilfe von Abb. 1 klar:
- Für P und Q ermittelt man gleich hohe Durchschnittswerte.
- Daraus folgt sofort: Auf einer Geraden durch den Ursprung ändern sich die Werte von x und y zueinander proportional. d. h., wenn der x-Wert verdoppelt wird, verdoppelt sich auch der y-Wert. Das bedeutet auch: Wenn der Wert von x um 1 % erhöht wird, dann steigt auch der Wert von y um 1 %. Die Gerade durch den Ursprung besitzt also eine konstante Elastizität von 1. Ihre Steigung spielt dabei keine Rolle (Ausnahme: sie verläuft waagerecht oder senkrecht).
- Ohne zu messen kann man auf den ersten Blick feststellen, dass der Durchschnittswert y/x in R größer ist als in P (und in jedem anderen Punkt auf der Gerade).
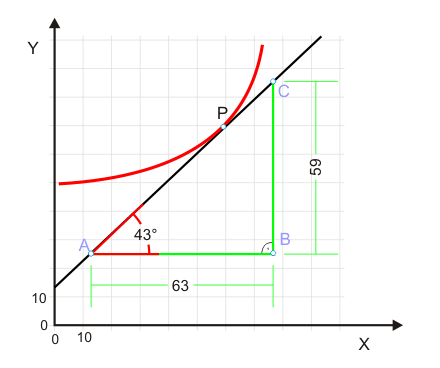
2. Und wie bestimmt man grafisch die Steigung einer Kurve?
Abbildung 2
3. Praktisches Beispiel:
Abbildung 3
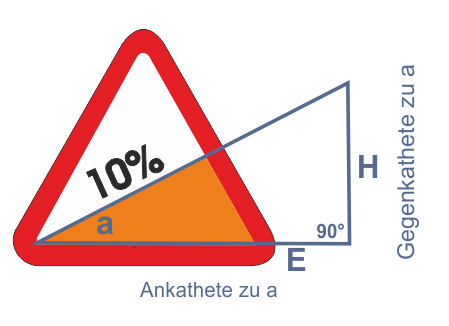
Und was hat das nun mit dem Durchschnitt zu tun? Ganz einfach: im Durchschnitt entfällt auf einen Meter ein Anstieg von einem Dezimeter (\(tan(a) = \frac {H} {E}\)).