Kleine Fehler akzeptieren

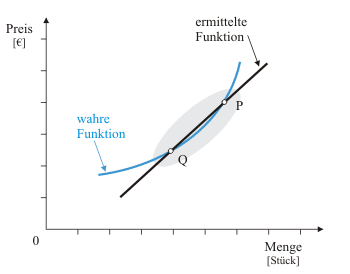
In vielen Fällen reicht es vollkommen aus, von linearen Zusammenhängen auszugehen, auch wenn die wahren Zusammenhänge nicht linear sind. Natürlich kennt man die wahren Zusammenhänge in der Regel nicht, aber angenommen wir wüssten, die wahre Angebotsfunktion eines Gutes wäre die blaue Funktion. Nun beobachten wir einen Forscher, dem es in mühevoller Arbeit gelingt, zwei Punkte (P, Q) dieser Funktion ausfindig zu machen. Aus den beiden Punkten konstruiert der Forscher die schwarze Angebotsfunktion.

Welchen Fehler macht der Forscher?

Es kommt darauf an. Solange sich zukünftige Ereignisse im Bereich der Punkte P und Q abspielen, ist sein Fehler nicht besonders groß (grauer Bereich). Je weiter zukünftige Beobachtungen sich jedoch von der grauen Ellipse entfernen, desto größer wird der Fehler. Wenn wir uns dessen bewusst sind (und bereit sind, kleinere Fehler in Kauf zu nehmen), könnten wir mit der Gerade als Annäherung an die wahre Funktion zufrieden sein. Vor allem, wenn wir uns in die Lage des Auftraggebers der Untersuchung versetzen. Die Ermittlung weiterer Stützpunkte würde zwar zu einer genaueren Ermittlung der wahren Funktion beitragen, aber auch Kosten verursachen. Wir müssten also abwägen, ob wir diese Kosten für einen im voraus schwer einschätzbaren Gewinn an Genauigkeit zu tragen bereit wären.