Aufgabenstellung:
Von einem Markt seien bekannt
- die Zahl der (identischen) Unternehmen = 1000,
- deren Kostenfunktionen $C = 2x^2$ und
- die Marktnachfrage $p = 400 - 0,004X$.
Dabei steht ein kleines $x$ steht für die Menge eines Unternehmens, ein großes $X$ für die Marktmenge.
Der Staat besteuert die Produktion mit einer Mengensteuer $t$ in Höhe von $80$ Geldeinheiten. Welche Auswirkungen hat die Steuer auf das Marktgleichgewicht?
Lösung:
Die hohe Zahl von 1000 identischen Unternehmen stellt in diesem Zahlenbeispiel Konkurrenz sicher. Die Kostenfunktion einer Unternehmung lautet
$$ C = 2x^2 \tag{1} $$Damit sind die Grenzkosten
$$ C' = 4x \tag{2} $$und nach der Preis-Grenzkosten-Regel lautet die individuelle Angebotsfunktion
$$ p = 4x \tag{3} $$Die hinreichende Bedingung für Gewinnmaximierung ist erfüllt, denn die Grenzkosten steigen an.
Eine einzelne Unternehmung möchte also die Menge
$$ x = \cfrac{p}{4} \tag{4} $$anbieten. Da es annahmegemäß 1000 identische Unternehmen im Markt gibt, lautet das Marktangebot
$$ X = 1000x = 250p \tag{5} $$oder
$$ p = \cfrac{X}{250} \tag{6} $$Mit der Marktnachfrage
$$ p = 400 - 0,004X \tag{7}$$findet man durch Gleichsetzen mit der Angebotsfunktion (6) das Marktgleichgewicht
$$ 400 - 0,004X = \cfrac{X}{250} \tag{8}$$ $$ X^* = 50.000 \tag{9} $$ $$ p^* = 400 - 0,004 \cdot 50.000 = 200 \tag{10} $$Diese Situation ist in Abbildung 1 wiedergegeben.
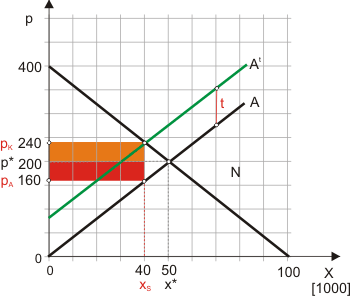
Auf ein einzelnes der 1000 Unternehmen entfällt eine Produktion von
$$ x^* = \cfrac{50.000}{1.000} = 50 \tag{11}$$Stück. Zu diesem Ergebnis hätte mit Kenntnis des Marktpreises in Höhe von 200 natürlich auch die Preis-Grenzkostenregel (3) geführt
$$ 200 = 4x \tag{12}$$Nun führt der Staat eine Mengensteuer
$$ t = 80 \tag{13}$$ein. Die Angebotsfunktion verlagert sich um den Steuerbetrag nach oben
$$ p = t + \cfrac{X}{250} \tag{14}$$Das neue Marktgleichgewicht berechnet man mit (14) und (7) zu
$$ 80 + \cfrac{X}{250} = 400 - 0,004X \tag{15}$$ $$ {X_t}^* = 40.000 \tag{16}$$ $$ {p_t}^* = 240 \tag{17}$$Die Steuer lässt den Preis auf 240 Geldeinheiten steigen und das gehandelte Volumen um 10.000 Einheiten sinken. Da jetzt noch 40.000 Stück gehandelt werden, beträgt die Steuereinnahme des Staates 3,2 Mio. Geldeinheiten.
Die einzelne Unternehmung produziert nun nur noch
$$ {x_t}^* = \cfrac{{X_t}^*}{1.000} = 40 \tag{18}$$Einheiten. Aus ihrer Sicht stellt sich die Kostensituation nun als
$$ C = 2x^2 + tx \tag{19} $$dar, so dass ihre Grenzkosten
$$ C' = 4x + t \tag{20} $$betragen und über die Preis-Grenzkostenregel die gewinnmaximierende Produktionsmenge zu
$$ 240 = 4x + 80 \tag{21} $$ $$ {x_t}^* = 40 \tag{22}$$errechnet wird.
In diesem Zahlenbeispiel "überleben" alle 1000 Unternehmen. Da sie aber weniger produzieren, benötigen sie weniger Produktionsfaktoren. Eine mittelbare Wirkung der Steuer in den Unternehmen sind also Entlassungen.
Wären die Unternehmen nicht identisch, hätte es natürlich mehr Mühe bereitet, die Auswirkungen der Steuer zu bestimmen. Technisch weniger effiziente Unternehmen hätte die Steuer härter getroffen. Sie hätten im Markt u.U. nicht überleben können.
Abschließend zu diesem kleinen Rechenexempel noch zwei Warnungen: Die Annahme, dass sich die Unternehmen in technischer Hinsicht unterscheiden, passt allerdings nicht gut zur Marktform vollkommener Konkurrenz. In dieser "perfekten Welt" müsste sich eigentlich in allen Unternehmen das kostengünstigste Produktionsverfahren durchgesetzt haben (keine Transaktionskosten, vollkommene Information). Und der Ehrlichkeit halber sei noch eine kleine Unzulänglich des Zahlenbeispiels zugegeben - wenn Sie es nicht schon selbst bemerkt haben: Die Unternehmen machen in der Ausgangssituation einen Periodengewinn von 5000 Geldeinheiten. Auch nach der Steuereinführung verbleibt jedem Unternehmen noch ein Gewinn von 3200 Geldeinheiten. Diese Gewinne müssten eigentlich weitere Wettbewerber in den Markt locken, wenn man nicht annehmen wollte, dass irgendwelche Markteintrittskosten dies verhinderten.