- Sie haben vor, die mikroökonomische Theorie des Arbeitsangebotes näher zu betrachten,
- Sie beabsichtigen, sich mit der Theorie des Allgemeinen Gleichgewichts oder
- mit der Reinen Theorie des Außenhandels zu beschäftigen.
Ob ein Markt nach einer Störung in ein Gleichgewicht zurückfindet, hängt offensichtlich davon ab, wie sich die Händler, also die Akteure, die das Gut kaufen und/oder verkaufen möchten, verhalten. Eine primitive Annahme wäre, dass kein Händler auf eine Parameteränderung in irgendeiner Art und Weise reagiert. Dann würde sich nach einer Störung kein neues Gleichgewicht einstellen können. Diese Verhaltensannahme lässt sich allerdings nicht aufrecht erhalten. Den Akteuren bleibt nämlich gar nichts übrig, als zu reagieren. Geht z.B. die Nachfrage dauerhaft zurück, dann können die Anbieter unmöglich an ihren bisherigen Produktionsplänen festhalten. Für einige wäre es der sichere Untergang.
Im folgenden werden die Stabilitätskonzepte nach Marshall und Walras betrachtet. Dazu wird zunächst eine Überschussnachfragefunktion (ÜN-Funktion) konstruiert, die für alternative Preise die Differenz zwischen Nachfrage- und Angebotsmenge zeigt.
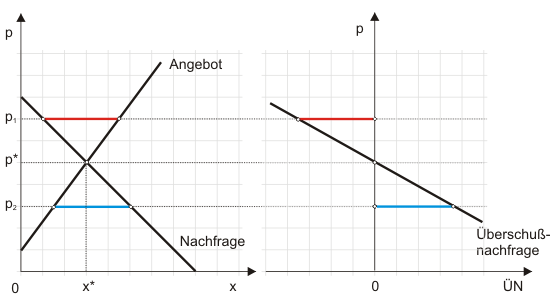
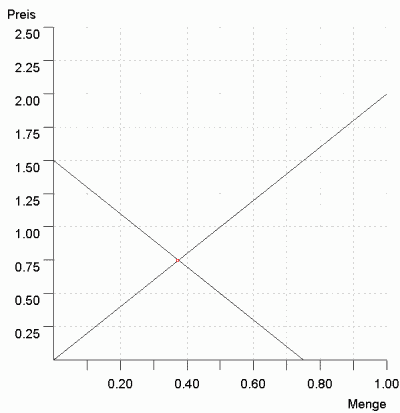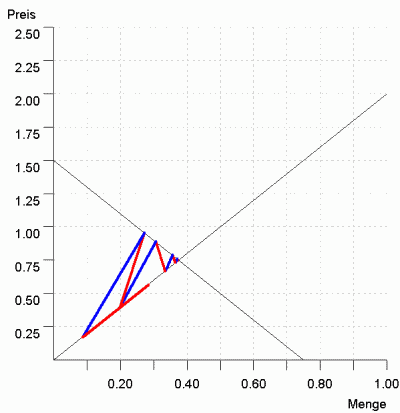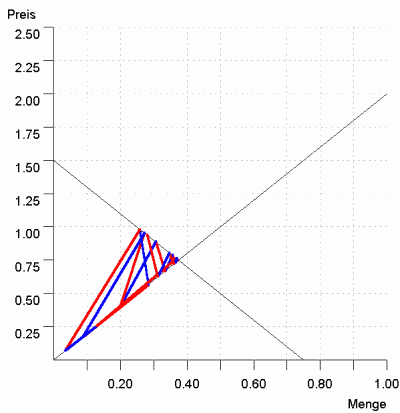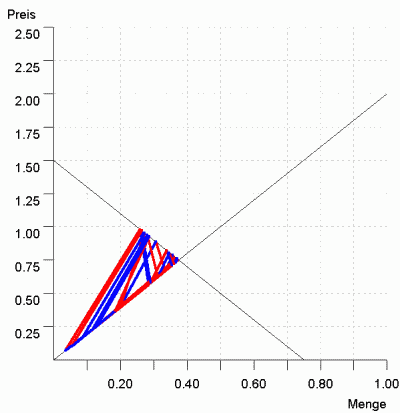
Tipp: Für ein kleines Land - klein in dem Sinn, dass es auf Preise auf dem Weltmarkt keinen Einfluss hat - können Sie die ÜN-Funktion als Exportangebots- bzw. als Importnachfragefunktion interpretieren. Bei einem Weltmarktpreis in Höhe $p_2$ fragt das Land die durch die blaue Strecke in Abbildung 1 angezeigte Menge auf dem Weltmarkt nach. Die Importnachfrage reagiert also elastischer auf den Preis als die Binnennachfrage. Entsprechendes gilt für das Exportangebot.
Die Konstruktion der ÜN-Funktion in Abbildung 1 erklärt sich eigentlich von selbst: Beim Gleichgewichtspreis ist die Überschussnachfrage null und mit fallendem Preis wird sie bei normal verlaufenden Angebots- und Nachfragefunktionen offensichtlich zunehmen. Eine negative Überschussnachfrage entspricht natürlich einem Überschussangebot. Beachtenswert und nicht mehr ganz so offensichtlich, aber auch noch mit der "Methode des genauen Hinsehens" ermittelbar, ist zudem die vergleichsweise hohe Elastizität der ÜN-Funktion.
Walrasianische Stabilität
Jetzt erscheint der viel zitierte Walrasianische Auktionator auf der Bühne. Er dient dazu, die Entscheidungen der Unternehmen abzubilden. Über Intelligenz verfügt er aber nicht. Er verhält sich wie ein programmierter Roboter: beobachtet er Preise oberhalb des Gleichgewichtspreises, ruft er niedrigere Preise aus und umgekehrt.
Die Vorstellung des Walrasianischen Auktionators hilft die Schwierigkeit zu umgehen, dass sich auf einem vollkommenen Wettbewerbsmarkt die einzelnen Akteure nur als Mengenanpasser verhalten können. Wer sollte aber die Preise anpassen, wenn nicht die Anbieter? Da ein einzelner Anbieter bei einer Preiserhöhung aber sofort seine gesamte Nachfrage an die Konkurrenten verlöre, stellt man sich den Preisanpassungsprozess so vor, dass alle Anbieter jeweils zu dem vom gedachten Auktionator ausgerufenen Preis anbieten.
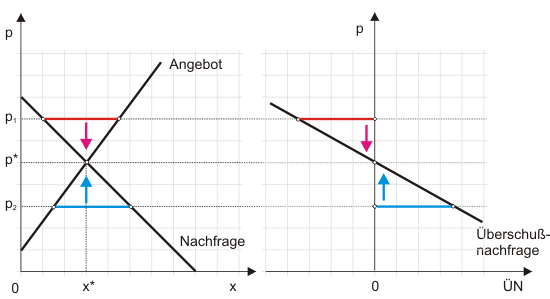
Wie Abbildung 2 zeigt, bewegen sich die Preise in Richtung des Gleichgewichtspreises. Allerdings ist ohne weitere Annahmen keine Aussage möglich, ob der Gleichgewichtspreis erreicht wird und, falls ja, wie lange der Preisanpassungsprozess dauert. Es wäre ja denkbar, dass der Auktionator "über das Ziel hinausschießt" und viel zu große Preisänderungen vornimmt. Wie im Cobweb-Modell könnte dies in einem Schweinezyklus enden oder die Preisschwankungen könnten explodieren. Trotzdem wird üblicherweise die Bewegung der Preise in die richtige Richtung als ausreichend angesehen, um von einem stabilen Markt zu sprechen. Der Markt in Abbildung 2 wäre demnach "walras-stabil".
Ohne dass etwas berechnet werden soll, wird sich zeigen, dass das einfache Niederschreiben des Auktionatorverhaltens in einer Gleichung den Prozess der Preisanpassung verdeutlichen hilft. Dazu sei $UN$ die Überschussnachfrage, die sich als Differenz aus Nachfragemenge $x^N$ und Angebotsmenge $x^A$ ergibt:
$$ p_t - p_{t-1} = f(UN) \space\space\space \text{mit} \space f' > 0 \space\space \text{und} \space\space f(0) = 0 \tag{1} $$Die Veränderung des gegenwärtigen Preises $p_t$ gegenüber der Vorperiode ist eine Funktion der Überschussnachfrage. Wenn die Überschussnachfrage null ist, soll sich der Preis nicht verändern, d.h., ist das Gleichgewicht einmal erreicht, kommt es nicht zu weiteren Preisanpassungen. Mit steigender Überschussnachfrage soll die Preisänderung zunehmen.
Das sind sicherlich auch sinnvolle Annahmen über das Verhalten von Unternehmen. Die einfachste konkrete Spezifikation der Preisanpassungshypothese wäre
$$ p_t - p_{t-1} = a \cdot UN \space\space\space \text{mit} \space a > 0 \tag{2} $$In der Höhe des Wertes für $a$ käme zum Ausdruck, wie stark die Anbieter auf eine Überschussnachfrage reagieren.
Angenommen $a=0,5$ und Nachfrage und Angebot seien bekannt als
$$ x^N = 10 - 3p \tag{3} $$ $$ x^A = p \tag{4} $$Durch Gleichsetzen findet man die Gleichgewichtsmenge $x^*= 2,5$ bei einem Gleichgewichtspreis von $p^* = 2,5$. Da ja untersucht werden soll, ob der Markt ins Gleichgewicht findet, sei angenommen, der Preis liege momentan bei $p_0 = 2$.
Da $UN = x^N - x^A$ ist, kann man (3) und (4) in (2) einsetzen:
$$ p_t - p_{t-1} = 0,5(x^N - x^A) \tag{5} $$ $$ p_t - p_{t-1} = 0,5(10 -4p) \tag{5} $$Für einen Preis von 2 berechnet man mit dem Klammerausdruck in (6) eine Überschussnachfrage von 2. Multipliziert mit dem Preisanpassungsparameter $a$ ergibt sich eine Preisänderung in Höhe von +1. Daher gilt $p_1 = p_0 + 1 =3$.
Mit einem Preis von 3 ergibt sich allerdings eine negative Überschussnachfrage in Höhe von -2, also ein Überschussangebot, und Gleichung (6) weist aus, dass die Anbieter den Preis um 1 senken werden. Damit ist der Preis wiederum so hoch wie in der Ausgangsperiode. Der Wert $a = 0,5$ führt also dazu, dass gerade ein Schweinezyklus auftritt. Mit weniger heftigen Preisreaktionen der Anbieter, die z.B. mit einem Wert $a = 0,4$ abgebildet werden könnten, würde man gedämpfte Schwingungen feststellen. Der Markt wäre also stabil.
Man kann nicht sicher sein, dass die Walrasianische Preisanpassung immer in die "richtige" Richtung läuft. M.a.W.: Wenn die Unternehmen bei einer Überschussnachfrage den Preis anheben, kann die Überschussnachfrage sogar noch zunehmen. Dazu müssen allerdings die Angebots- oder Nachfragefunktion einen untypischen Verlauf zeigen. Das Beispiel in Abbildung 3 zeigt einen solchen walras-instabilen Markt:
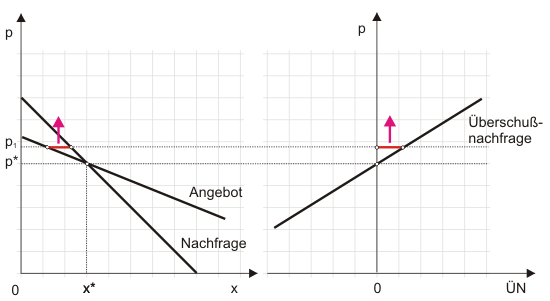
Dieses Resultat muss aber nicht zwangsläufig eintreten, wenn die Angebotsfunktion untypisch verläuft. Besäße sie im Unterschied zu Abbildung 3 im Gleichgewicht eine geringere Elastizität als die Nachfragefunktion, dann würde die ÜN-Funktion im rechten Teildiagramm wie in Abbildung 2 fallenden Verlauf zeigen und Preiserhöhungen würden die Überschussnachfrage abbauen.
Ausgeschlossen ist eine (in Teilbereichen) fallende Angebotsfunktion nicht. Ein populäres Beispiel findet sich in der Arbeitsangebotsentscheidung des privaten Haushalts. Mit steigenden Löhnen (= Preis der Freizeit) nimmt die Nachfrage nach Freizeit zunächst ab und somit das Arbeitsangebot (= Zeitbudget minus Freizeit) zu. Während bei niedrigen Löhnen dieser Substitutionseffekt durchschlägt, gewinnt der Einkommenseffekt der Freizeitnachfrage bei steigenden Löhnen zunehmend an Bedeutung. Mit steigendem Lohnsatz steigt das Einkommen des Haushalt und - weil Freizeit sicherlich ein superiores Gut ist - nimmt c.p. die Nachfrage nach Freizeit zu. Gewinnt dieser Effekt Überhand, kommt es bei der Arbeitsangebotsfunktion des einzelnen Haushalts zu einem rückwärts geneigten Teil ("backward bending labor supply curve"). dass der Effekt auch beim aggregierten Arbeitsangebot zu beobachten ist, dürfte aber eher unwahrscheinlich sein, da mit steigenden Löhnen natürlich die Erwerbsneigung zunehmen wird.
Auch mit dem sogenannten Veblen-Effekt lässt sich (unter einigen Verrenkungen) eine untypische, nämlich ansteigende, Nachfragefunktion konstruieren. Der Veblen- oder Prestige-Effekt behauptet, dass Konsumenten aus demonstrativem Konsum ("Gott, was kann der sich alles leisten!") Nutzen ziehen, weil sie sich daran delektieren, dass andere sie beneiden. Da der Neid um so größer ist, je höher der Preis des Gutes ist, wird der Preis quasi selbst zur nachgefragten Eigenschaft.
Marshall-Stabilität
Im Unterschied zu Walras stellt bei Marshall nicht der Preis, sondern die Menge die Aktionsvariable der Anbieter dar. Das geht insofern mit der Theorie vollkommener Wettbewerbsmärkte konform, dass die Händler Mengenanpasser sind. In Marshalls Analyse sind die Begriffe Nachfrage- und Angebotspreis zentral. Unter dem Nachfragepreis versteht er jenen Preis, zu dem die Nachfrager in der betrachteten Periode die gegebene Menge an Gütern zu kaufen bereit sind. Eine größere Menge würde von den Nachfragern nur zu einem geringeren Preis gekauft werden, so dass der Nachfragepreis mit steigender Menge fällt.
Analog definiert er den Angebotspreis. Wenn die für die Branche repräsentative Unternehmung diesen Preis erwartet, dann ist sie gerade (noch so) bereit, an der aktuell produzierten Menge festzuhalten. Manche Unternehmen mögen die Produktion bei diesem erwarteten Preis senken, andere mögen die Produktion ausdehnen, aber das Marktangebot ändert sich bei diesem Preis gerade nicht.
Marshall spricht hier quasi nebenbei eine Selbstverständlichkeit an, der heute in der ökonomischen Theorie mitunter nicht die notwendige Aufmerksamkeit geschenkt wird (Principles V.III.§4). Es ist ganz natürlich, dass in einer Branche, zeitgleich einige Unternehmen schrumpfen, während andere wachsen. Die Konzentration auf die "repräsentative" Unternehmung verleitet jedoch dazu, alle Unternehmen als gleich aufzufassen. Wenn in einer Industrie mit 100 Unternehmen die Produktion um 1000 Einheiten zurückgeht, entfällt aber nur im Durchschnitt auf jede Unternehmung ein Produktionsrückgang um 10 Einheiten. Manche schrumpfen stärker und manche schwächer. Bei wiederum anderen kann die Produktion auch zugenommen haben.
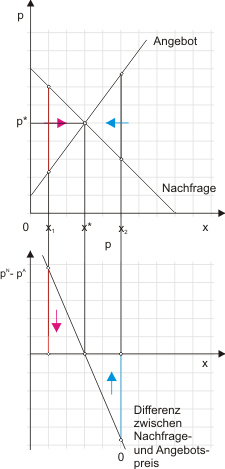
Wenn der Nachfragepreis nun über dem Angebotspreis liegt, erzielen die Unternehmen höhere Preise, als zur Aufrechterhaltung der Produktion auf gegenwärtigem Niveau notwendig wäre. Das wird für sie Anlass sein, ihre Produktion auszudehnen. Mit der steigenden Produktion bewegen sich Angebots- und Nachfragepreis aber aufeinander zu. Die Schere schließt sich. In Abbildung 4 ist diese Situation dargestellt. Für die Menge $x_1$ liegt der Angebotspreis $p_A$ unter dem Nachfragepreis $p_N$. Die Anbieter reagieren mit einer Ausweitung der Produktion. Genau umgekehrt ist es bei der Menge $x_2$: der Angebotspreis liegt über dem Nachfragepreis, was die Anbieter als Signal nehmen, die Produktion zurückzufahren.
Ein (extremes) Beispiel: Von 1997 auf 1998 hat die Arbeitslosigkeit um ca. 100 Tausend Personen abgenommen (Durchschnittswert). 1998 gab es aber über 7 Millionen Zugänge in Arbeitslosigkeit.
Wie bei der Walras-Stabilität zeigt sich auch bei der Marshall-Stabilität, dass bei atypisch verlaufenden Angebots- und Nachfragefunktionen die Anpassungsprozesse vom Gleichgewicht weg führen können. Ohne die Fälle im einzelnen zu untersuchen, sei festgehalten, dass Märkte, die Walras-stabil sind, Marshall-instabil sind und umgekehrt.
Chaotische Anpassungsprozesse
In Gleichung (2) ist die walrasianische Anpassungshypothese so spezifiziert, dass die Anbieter die Preise von Periode zu Periode in Abhängigkeit von der Überschussnachfrage absolut anheben oder senken. Eine kleine Modifikation dahingehend, dass die Anbieter die Preise nicht absolut,
$$ \cfrac{p_t - p_{t-1}}{p_t} = a\cdot UN \space \space \space \text{ mit } \space \space \space a>0 \tag{7}$$sondern wie in Gleichung (7) relativ verändern, führt zu einem interessanten Ergebnis: Bei bestimmten Parameterkonstellationen treten chaotische Preisanpassungspfade auf. Abbildung 5 zeigt ein entsprechendes Zahlenbeispiel über 30 Perioden.
Die Abbildung zeigt eine walrasianische Anpassung über 30 Perioden: Die Anbieter variieren den Preis prozentual in Abhängigkeit von der Überschussnachfrage; Start nahe Gleichgewicht $p = 0.745$, $p^* = 0.75$; Anpassungsparameter $a = 4$.
Angebotsfunktion: $p = 2x$;
Nachfragefunktion: $p = 1,5 - 2x$
Erstaunlich ist, dass die scheinbar unerhebliche Änderung der Verhaltensannahme zu so deutlich qualitativ verschiedenen Ergebnissen führt. Zudem besitzt die chaotische Preisbewegung selbst einige überraschende Eigenschaften. So kann es z.B. sein, dass der Preis dem Gleichgewichtspreis extrem nahe kommt, sich dann wie aus heiterem Himmel wieder deutlich von diesem entfernt. Ebenso kann der Fall auftreten, dass sich die Muster der Bewegung nicht wiederholen (auch mehrperiodige Zyklen sind möglich). Selbst bei genauer Kenntnis der Preisentwicklung in der Vergangenheit ist dann nicht einmal Prognose des Preises in der nächsten Periode möglich.
Nach ähnlichen Seiten im WWW suchen
