Diese Seite funktioniert nur mit Javascript.
Die Positive Theorie5.1.1 Die Edgeworth-BoxKontraktkurve und Kern
ie sogenannte Edgeworth-Box stammt weder von Edgeworth (1845-1926) noch handelt es sich um eine Box, denn sie besitzt nur zwei Dimensionen. Tatsächlich geht sie zurück auf Pareto. Ihren heutigen Namen hat sie erhalten, da Marshall (1842-1924) sie in seinen "Principles of Economics" nach einem wissenschaftlichen Disput mit Edgeworth (fälschlicherweise) so bezeichnete. Edgeworth hat sich jedoch mit dem Themenkreis so intensiv beschäftigt, dass man heute auch ruhigen Gewissens behaupten darf, die Box sei ihm zu Ehren so benannt. Geläufige Synonyme sind Tauschbox, Edgeworth-Bowley-Box und Schachteldiagramm.
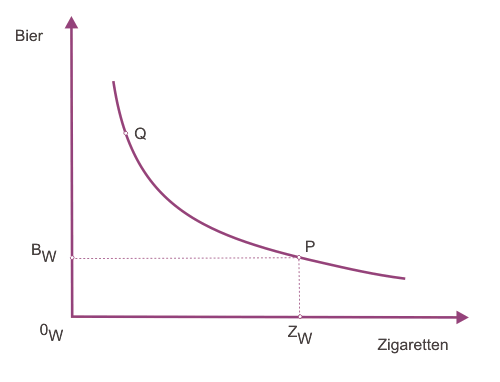
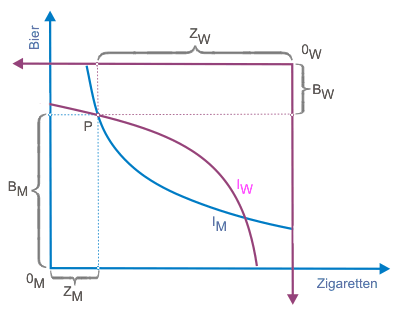
Betrachten wir zunächst eine Darstellung, die aus der Haushaltstheorie bekannt ist. Abbildung 1 zeigt eine Indifferenzkurve, auf der sich der Konsument befindet, wenn er über die eingezeichneten Mengen der Güter Bier und Zigaretten verfügt.

Statt den Beschwerdebrief in den Papierkorb zu werfen, hat das Ministerium vom Dekan des Fachbereichs eine Stellungnahme eingefordert. Das Drama fand aber ein gutes Ende. Der Kollege blieb im Dienst. Was aus dem Studenten wurde, kann ich leider nicht berichten. Die Beschwerde war anonym.
Natürlich könnten wir die Güter auch x und y oder sonst irgendwie nennen. "Bier" und "Zigaretten" kann man sich gut merken und besser auseinanderhalten als zum Beispiel Gut 1 und Gut 2. Das ist der einzige Grund für die Wahl dieser beiden Güter.
Punkt P zeigt die (Anfangs)Ausstattung des Konsumenten mit Bier und Zigaretten. Er befindet sich auf dem Nutzenniveau, das durch die Indifferenzkurve IM angezeigt wird. Der Index M soll anzeigen, dass es sich um den Konsumenten (M für männlich) handelt. Für die Konsumentin wird im folgenden der Index W stehen.
Alle Annahmen, die bei der Ableitung des Haushaltsgleichgewichts Anwendung finden, werden auch hier getroffen. Die ordinalen Nutzenfunktionen der Individuen sind aus einer reflexiven, vollständigen und transitiven Präferenzordnung abgeleitet und die Güter sind sowohl homogen als auch beliebig teilbar. Daneben ziehen alle Individuen Güterbündel, die von mindestens einem Gut mehr enthalten und von keinem anderen weniger, anderen Güterbündeln strikt vor (Nichtsättigung). Transaktionskosten entstehen nicht, da eine zeitlose Punktwirtschaft unterstellt wird. Um Einkommen und Güterpreise wollen wir uns hier noch nicht kümmern. Es wird angenommen, dass der Konsument (M) in der betrachteten Periode über die Mengen BM an Bier und ZM an Zigaretten verfügen kann.
Fände der Konsument irgendeinen Tauschpartner, mit dem er Bier und Zigaretten in dem durch die Gerade g angezeigten Verhältnis tauschen könnte, dann hätte der Konsument sein Haushaltsgleichgewicht nicht erreicht, da eine höhere Indifferenzkurve erreichbar wäre. Bestünde die Möglichkeit, würde er Bier gegen Zigaretten eintauschen. In den Worten der Haushaltstheorie würde er diesen Tausch tätigen, weil das offerierte Tauschverhältnis von seiner (umgekehrten, absoluten) Grenzrate der Substitution abweicht.
Denken Sie daran, dass die Grenzrate der Substitution anzeigt, in welchem Verhältnis der Konsument bei Indifferenz Bier gegen Zigaretten zu tauschen bereit ist. Falls Ihnen dies nicht klar ist, lesen Sie es hier noch einmal nach, da dem Begriff der Grenzrate der Substitution im Folgenden eine zentrale Bedeutung zukommt.
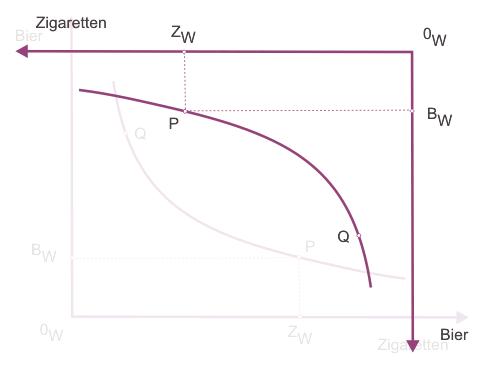
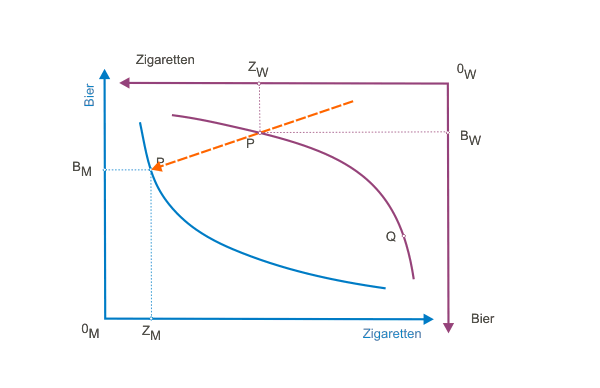
Abbildung 2 zeigt die gleiche Darstellung für die Konsumentin (W für weiblich). In ihrer Anfangsausstattung verfügt sie über relativ (und absolut) mehr Zigaretten und weniger Bier als der Konsument. Die entsprechende Indifferenzkurve ist von anderer Gestalt, da sie eine andere Nutzenfunktion als er besitzen soll. Es ist übrigens nicht notwendig, dass ihr sowohl eine andere Anfangsausstattung als auch eine andere Nutzenfunktion zugewiesen wird, in einem von beiden sollte sie sich allerdings vom Konsumenten unterscheiden. Es ist leicht einzusehen, dass sich im gegenteiligen Fall die Gesellschaft bereits in einer gleichgewichtigen Situation befände, in der wir keine Aktionen beobachten könnten.
Wenn in beiden Abbildungen die Skalierung der Achsen übereinstimmt, ist für die Konsumentin eine andere Grenzrate der Substitution zwischen Bier und Zigaretten zu erkennen als für den Konsumenten. Gemessen in Zigaretten ist Bier für die Konsumentin teurer. Dies gilt allerdings nur für die jeweils durch P angezeigten verfügbaren Mengen für beide Personen. Verfügte die Konsumentin demgegenüber über die durch Q angezeigten Mengen, hätte sich infolge des Gesetzes der abnehmenden Grenzrate der Substitution ihre relative Wertschätzung der Güter zugunsten von Zigaretten geändert.
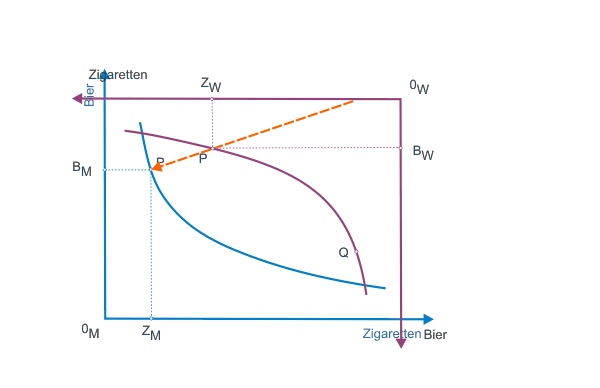
Um in der weiteren Analyse nicht ständig wechselnd die Abbildungen 1 und 2 betrachten zu müssen, wird in Abbildung 3 die Edgeworth-Box konstruiert. Dazu drehen wir zunächst das Diagramm in Abb. 2 um 180°. Wie es dann aussieht, können Sie sich in der klickbaren Abbildung 2 ansehen. Damit Sie den Text nicht auf dem Kopf lesen müssen, ist die Beschriftung gleich wieder richtig eingetragen.
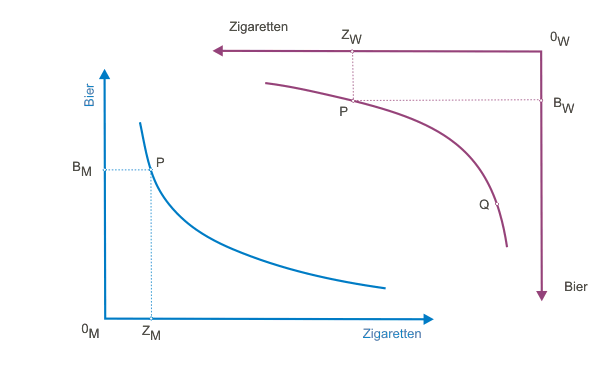
Im nächsten Schritt legen wir das gedrehte Diagramm für die Konsumentin versetzt neben das Diagramm für den Konsumenten aus Abbildung 1. Die Ordinaten und Abszissen werden parallel zueinander ausgerichtet.
Das gedrehte Diagramm aus Abbildung 2 wird mit dem Diagramm aus und Abbildung 1 kombiniert.
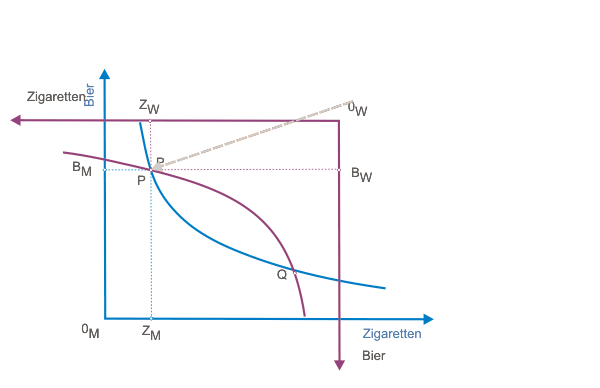
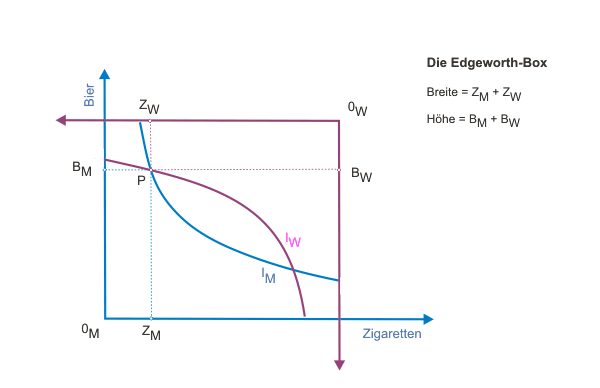
Anschließend werden die beiden Punkte P übereinandergeschoben, wobei die Abzissen und Ordinaten zueinander parallel gehalten werden. Dadurch entsteht das Rechteck der Abbildung 3 mit der Länge ZM + ZW und der Höhe BM + BW. Die klickbare Abbildung 3 zeigt die Konstruktion. Das fertige Diagramm sehen Sie in Abb. 3a.
Die Linse, die durch die beiden Indifferenzkurven entstanden ist, wird auch so genannt.
Beide Gesellschaftsmitglieder würden dort jeweils eine höhere Indifferenzkurve erreichen (durch die Drehung liegen höhere Indifferenzkurven der Konsumentin nun de facto niedriger). Alle Punkte auf dem Rand der Linse, ausgenommen der zweite Schnittpunkt, zeichnen sich dadurch aus, dass jeweils eines der Gesellschaftsmitglieder einen solchen Punkt präferierte, während das andere indifferent wäre. Alle Punkte außerhalb der Linse würden jeweils von mindestens einem der beiden schlechter bewertet als die durch P angezeigte Situation.
Nach dem Pareto-Kriterium würden daher in der Edgeworth-Box alle Punkte in der Linse und auf ihrem Rand (und nur diese) dem Punkt P vorgezogen. Diese Punkte nennt man dementsprechend pareto-superior gegenüber P.
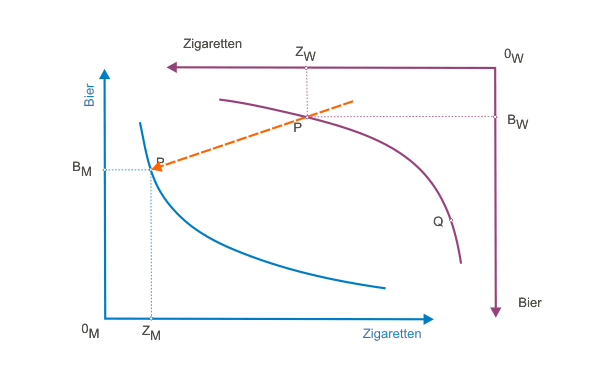
Uns als Betrachter der Situation wäre es nun ohne Weiteres möglich, eine Umverteilung von Bier und Zigaretten vorzunehmen, die die Zustimmung beider Gesellschaftsmitglieder finden würde. Wir bräuchten dazu nur einen Punkt in der Linse auszuwählen. Der Konsument erhielte mehr Zigaretten und müsste dafür Bier aufgeben. Die Konsumentin erhielte Bier und müsste Zigaretten aufgeben. Durch die Betrachtung der Grenzraten der Substitution (die in P gelten) ist ja bereits bekannt gewesen, dass der Konsument einem Glas Bier einen Gegenwert von weniger Zigaretten beimisst als die Konsumentin. Als Ergebnis kann festgehalten werden:
Wenn eine "übergeordnete Instanz" tatsächlich einen neuen Punkt in der Linse festlegt, sind prinzipiell zwei verschiedene neue Situationen denkbar. Zum einen kann es sich wiederum um einen Punkt handeln, in dem sich zwei Indifferenzkurven schneiden (Q in Abbildung 4), zum anderen um einen Punkt, bei dem sich zwei Indifferenzkurven tangieren (K in Abbildung 4).

Kommt ein Punkt wie Q zustande, gelten alle Überlegungen, die wir soeben für P angestellt haben. Für K jedoch kann kein weiterer pareto-superiorer Punkt gefunden werden, da jede Veränderung aus K heraus zwar ein Individuum besser, das andere jedoch schlechter stellen würde.
Dass eine weitere Umverteilung der Güter nicht ein Individuum besser stellen kann, ohne das andere zu schädigen, liegt an den nun übereinstimmenden Grenzraten der Substitution. Konsument und Konsumentin bewerten nun beide ein Glas Bier mit derselben Menge Zigaretten. Da die Grenzrate der Substitution abnimmt, müsste der Konsument, um indifferent zu bleiben, von der Konsumentin mehr Zigaretten für einen Liter Bier erhalten, als diese bei Indifferenz im Gegenzug zu geben bereit wäre. Die Situation ist vergleichbar einer besonderen Konstellation beim Kartenspiel "Schwimmen": Beide Spielpartner können sich durch den Austausch einer Karte nur verschlechtern. Keiner hat Anlass zu handeln. Es besteht ein Gleichgewicht.