Diese Seite funktioniert nur mit Javascript.
Minimalkostenkombination3.3.1 IsokostengeradeExpansionspfad
Die Kosten $C$ für die Produktionsfaktoren Arbeit $L$ und Kapital $K$ betragen
$$ C = wL + rK \tag{1}$$wobei $w$ den Lohnsatz (Preis für eine Einheit Arbeit) und $r$ den Zinssatz (Preis für eine Einheit Kapital) angibt. Etwas präziser wäre es, von Arbeits- und Kapitalnutzungskosten je Einheit zu sprechen, da aus Sicht des Unternehmens für den Einsatz der Produktionsfaktoren letztlich entscheidend ist, welche Kosten dadurch entstehen. Als Lohn wird also nicht aufgefasst, was die Arbeitskraft erhält, sondern was der Einsatz einer Einheit Arbeit in der Unternehmung (im Durchschnitt) kostet.*
Löst man Gleichung (1) nach $K$ auf und gibt einen Wert für die Kosten $C$ vor, erhält man eine Isokostengerade wie in Abbildung 1.

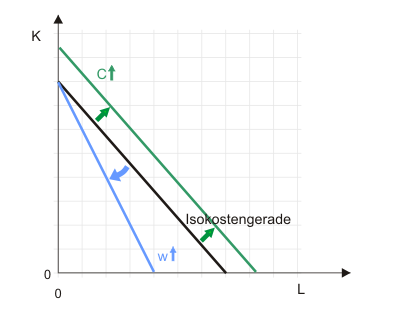
Da Isokostengeraden vollkommen analog zu Budgetgeraden in der Haushaltstheorie konstruiert werden, kann auf die entsprechenden Erklärungen dort verwiesen werden.
Wird eine Isokostengerade in ein Isoquantendiagramm eingezeichnet, lässt sich die maximal mit den gegebenen Kosten erreichbare Produktionsmenge offensichtlich durch die Isoquante feststellen, die von der Isokostengerade tangiert wird. Das ist in Abbildung 2 im Punkt P der Fall.
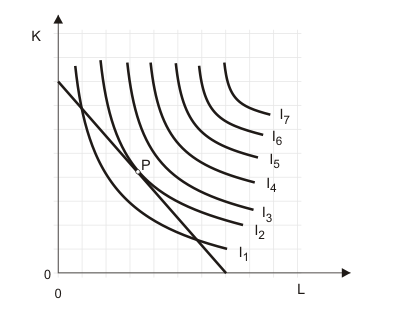
Punkt P zeigt eine Minimalkostenkombination.
Da die Steigung der Isoquante die Grenzrate der technischen Substitution anzeigt und die Steigung der Isokostengerade durch das Faktorpreisverhältnis bestimmt wird, lässt sich formulieren:
Die Grenzrate der technischen Substitution stimmt wiederum mit dem (negativen, umgekehrten) Verhältnis der Grenzproduktivitäten der Faktoren überein, so dass zudem gilt:
Die formale Ableitung dieser Aussagen kann auf zwei Wegen erfolgen. Entweder werden die Kosten unter der Nebenbedingung einer gegebenen Produktionsmenge minimiert oder die Produktionsmenge wird für gegebene Kosten maximiert. Der zweite Weg ist formal identisch mit der Herleitung des Haushaltsgleichgewichts (Maximierung des Nutzens bei gegebenem Einkommen und gegebenen Güterpreisen). Die notwendige Bedingung für die Minimalkostenkombination lautet
$$ -\frac{\mathrm{d}K}{\mathrm{d}L}=\frac{\cfrac{\partial x}{\partial L}}{\cfrac{\partial x}{\partial K}}=\frac{w}{r} \tag{2}$$Wenn man diese Bedingung umformt
$$ \cfrac{\cfrac{\partial x}{\partial K}}{r}=\cfrac{\cfrac{\partial x}{\partial L}}{w} \tag{3} $$kann man sie einfacher interpretieren: Auf der linken Seite der Gleichung steht die Grenzproduktivität des Kapitals pro Euro - also der Anstieg der Produktionsmenge, der mit dem letzten Euro erzielt wird, die für Kapital ausgegeben wird. Wenn diese Steigerung größer wäre, als die Produktionssteigerung, die mit dem letzten Euro erzielt wird, die für Arbeit ausgegeben wird, dann würde es sich lohnen, einen Euro weniger für Arbeit und einen Euro mehr für Kapital auszugeben. Die Kosten blieben dann gleich, aber die Produktion würde steigen.
Wird aber der Kapitaleinsatz ausgedehnt, dann sinkt - vorausgesetzt das Gesetz der abnehmenden Ertragszuwächse gilt - die Grenzproduktivität des Kapitals. Gleichzeitig steigt infolge des verminderten Arbeitseinsatzes die Grenzproduktivität der Arbeit. Der Substitutionsprozess von Arbeit durch Kapital führt somit zu einer Angleichung der Grenzproduktivitäten pro Euro. Wenn schließlich die in Gleichung (3) beschriebene Situation hergestellt ist, kann die Produktion bei gegebenen Kosten nicht mehr weiter ausgedehnt werden.
Das bedeutet auch eine Abhängigkeit des optimalen Faktoreinsatzes von den Faktorpreisen. Wenn in (3) der Lohnsatz w steigt, dann wird der Kapitaleinsatz auf Kosten des Arbeitseinsatzes ausgedehnt, um wieder einen kostenminimalen Faktoreinsatz zu erreichen. Diese wirtschaftspolitisch wichtige Feststellung gilt natürlich nur ceteris paribus, schließlich entstammt sie einem Partialmodell. Wie stark so ein Substitutionsprozess ausfällt, hängt von der Krümmung der Isoquanten ab. Darin kommt zum Ausdruck, wie einfach oder schwierig es technisch ist, die Produktionsfaktoren gegeneinander zu ersetzen. Im Fall einer Leontief-Produktionsfunktion mit rechteckigen Isoquanten ist die Substitution technisch ausgeschlossen [s. Abbildung 3].
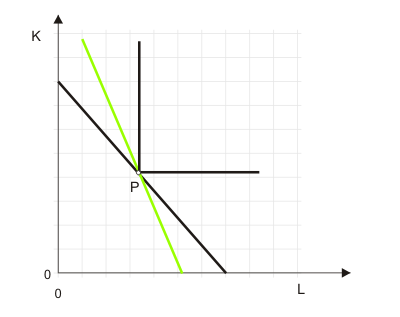
- Warum werden Anpassungen an Faktorpreisänderungen langfristig stärker ausfallen als kurzfristig?
- Wie müssten wohl die Isoquanten aussehen, die dazu führen können, dass die kleinste Veränderung der Faktorpreise einen vollkommenen Austausch eines Faktors durch einen anderen bewirkt?
- Machen Sie sich klar, wie im Fall perfekter Substitute die Isoquanten aussehen und dass es bei der Minimalkostenkombination zu Randlösungen kommt.
Bei anderen Produktionsfunktionen wird es aber zu Anpassungen kommen, von denen man vermuten kann, dass sie sich langfristig stärker auswirken als auf kurze Sicht. Im Extremfall perfekt substituierbarer Faktoren werden beide nur dann beschäftigt, wenn ihre Faktorpreise übereinstimmen. Bereits geringfügige Faktorpreisänderungen können hier starke Substitutionsvorgänge auslösen.
Wie stark die Reaktion im einzelnen ausfällt, hängt augenscheinlich von der Krümmung der Isoquanten ab. Ob und wenn ja, wie stark, Veränderungen im Faktorpreisverhältnis das Faktorpreiseinsatzverhältnis beeinflussen, wird mit der so genannten Substitutionselastizität gemessen (die optisch in der Krümmung der Isoquanten zum Ausdruck kommt). Eine genauere Betrachtung würde hier aber zu weit führen. Bei der Leontief-Produktionsfunktion in Abbildung 3 beträgt die Substitutionselastizität übrigens - Sie haben es richtig vermutet - null.
Nach ähnlichen Seiten im WWW suchen