Isokostengerade

3.3.2 Expansionspfad

Kostenfunktion

Graphisch kann man ihn erzeugen,  indem man mit geringen Kosten beginnend die Kosten langsam ansteigen läßt. Dadurch verschiebt sich die Isokostengerade weiter und weiter nach außen und tangiert eine Isoquante nach der anderen. Die Tangentialpunkte werden markiert und verbunden. Im Ergebnis entsteht ein Expansionspfad wie in Abbildung 1.

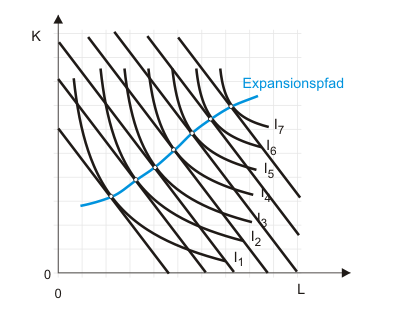
Natürlich ändert sich der Expansionspfad, wenn sich das Faktorpreisverhältnis verändert. Auch über seine Gestalt kann man a priori nicht allzu viel sagen. Allerdings zeigen bestimmte Gruppen von Produktionsfunktionen typische Expansionspfade. Die Leontief-Produktionsfunktion besitzt einen linearen Expansionspfad. Das muß natürlich so sein, denn bei einer limitationalen Produktionsfunktion wird das Einsatzverhältnis der Faktoren (die Kapitalintensität) allein durch die Technik konstant vorgegeben.

Etwas überraschender mag schon sein, daß auch eine Cobb-Douglas-Produktionsfunktion einen linearen Expansionspfad besitzt. Das kann nur der Fall sein, wenn die Grenzrate der Substitution (Steigung der Isoquanten) unabhängig vom Skalenniveau (der Produktionshöhe) ist. Das Verhältnis der Grenzproduktivitäten darf also nicht mit der Produktionsmenge variieren. Für die Cobb-Douglas-Produktionsfunktion $x = cK^aL^b$ berechnet werden

$$ - \cfrac{\text{d}K}{\text{d}L} = \frac{\cfrac{\partial x}{\partial L}}{\cfrac{\partial x}{\partial K}}=\frac{bcK^aL^bL^{-1}}{acK^aL^bK^{-1}}=\frac{b}{a}k \space \space \space \text{mit} \space k=\cfrac{K}{L} \tag{1} $$

Die Grenzrate der technischen Substitution hängt nur von den beiden partiellen Produktionselastizitäten und der Kapitalintensität $k$ ab. Die Kapitalintensität ist aber auf einer Geraden durch den Ursprung konstant und die beiden Produktionselastizitäten sind ebenfalls Konstanten. Damit ist die Grenzrate der technischen Substitution also auf einer Geraden durch den Ursprung konstant, m.a.W. die Steigung der Isoquanten ändert sich nicht. Der Expansionspfad hängt damit vom Verhältnis der partiellen Produktionselastizitäten ab und fällt bei gleichen Faktorpreisen ($w = r$) mit der 45°-Linie zusammen, wenn $a = b$ gilt. Allgemein gilt (siehe Gleichgewichtsbedingung)

$$ \frac{\cfrac{\partial x}{\partial L}}{\cfrac{\partial x}{\partial K}} = \cfrac{b}{a} \cfrac{K}{L} = \cfrac{w}{r} \tag{2}$$ $$ K = \cfrac{w}{r} \cfrac{a}{b} L \tag{3}$$

gleichung (3) ist der Expansionspfad für die Cobb-Douglas-Produktionsfunktion $x = cK^aL^b$. Die kostenminimale Kapitalintensität ist erwartungsgemäß um so höher, je produktiver Kapital im Verhältnis zur Arbeit ist, d.h. die Kapitalintensität ateigt mit $a/b$, und je höher die Lohn-Zins-Relation $w/r$ ausfällt.

Auch hier liegt - ceteris paribus natürlich - wieder eine wirtschaftspolitische Implikation auf der Hand: Eine Steigerung der Arbeitsproduktivität wird die Unternehmen aus eigenem Interesse arbeitsintensivere Produktionsverfahren wählen lassen.