Kurz- und langfristige Angebotsfunktion

3.5.1.2 Faktornachfrage

Angebotsfunktion einer Branche

at man die optimale Produktionsmenge über die Angebotsfunktion bestimmt, kann man auf den notwendigen Einsatz der Produktionsfaktoren zurückrechnen. Das am Ende dieses Abschnitts verlinkte Zahlenbeispiel wird dies deutlich machen. Da man aus der optimalen Produktionsmenge über den Expansionspfad den optimalen Faktoreinsatz ableiten kann, spricht man auch von abgeleiteter Faktornachfrage.

Bisher wurde das Problem der gewinnmaximierenden Produktion von der Outputseite aus betrachtet, denn die Frage lautete: Welche Menge wird das Unternehmen anbieten? Und die Antwort darauf heißt, wie jetzt bekannt ist: die Menge, die die Grenzkosten mit dem Preis in Übereinstimmung bringt.

Nun kann man das Problem aber ebenso von der Inputseite aus angehen und fragen: Welche Faktormengen wird ein Unternehmen einsetzen? Zur Beantwortung dieser Frage sei angenommen, Arbeit $L$ sei der einzige kurzfristig variable Produktionsfaktor. Der Lohnsatz pro Arbeitseinheit sei $w$. Die übrigen Produktionsfaktoren führen zu Fixkosten in Höhe von $F$. Der Gewinn kann dann angegeben werden als

$$ G(L) = p_xx(L) - wL - F \tag{1} $$

Die notwendige Bedingung für ein Gewinnmaximum findet man durch Nullsetzen der ersten Ableitung.

$$ \cfrac{\text{d}G(L)}{\text{d}L} = p_x\cfrac{\text{d}x(L)}{\text{d}L} - w \space {\overset{!}{=}} \space 0 \tag{2} $$ $$ p_x\cfrac{\text{d}x(L)}{\text{d}L} = w \space\space\space\space \Leftrightarrow \space \space \space \space \cfrac{\text{d}x(L)}{\text{d}L} = \cfrac{w}{p_x} \tag{3} $$

Der linke Term in Gleichung (3) zeigt das mit dem Marktpreis bewertete Grenzprodukt der Arbeit. Dies ist der wertmäßige Beitrag der letzten eingesetzten Arbeitseinheit zum Umsatz der Unternehmung und heißt Wertgrenzprodukt (der Arbeit).

$$ \cfrac{\text{d}^2G(L)}{\text{d}L^2} = p_x\cfrac{\text{d}^2x(L)}{\text{d}L^2} \space {\overset{!}{\lt}} \space 0 \tag{4} $$

Gleichung (4) zeigt die hinreichende Bedingung. Das (bewertete) Grenzprodukt der Arbeit muss abnehmen. Das ist der Fall, wenn für Arbeit das Gesetz von der abnehmenden Grenzproduktivität gilt. Zusammen mit der Wertgrenzproduktregel in Gleichung (3) lässt dies folgende einfache Interpretation zu: ein Produktionsfaktoreinsatz wird ausgedehnt, solange das Wertgrenzprodukt über dem Faktorpreis liegt - oder umgangssprachlich:

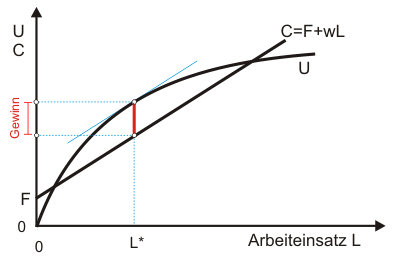
Umgekehrt gilt natürlich, dass Entlassungen den Gewinn erhöhen, wenn die physische Grenzproduktivität unter dem Reallohn liegt (s. rechte Gleichung in (3)). Abbildung 1 zeigt die Wertgrenzproduktregel.

Gleichung (3) zeigt an, dass das Grenzprodukt der Arbeit in einer gewinnmaximierenden Unternehmung dem Reallohn (w/p) angepasst wird.

Das ist bei einem abnehmenden Grenzprodukt aber nur durch eine Verminderung des Arbeitseinsatzes möglich. Gleichung (3) zeigt also, wie Lohnhöhe und Arbeitseinsatz miteinander im Zusammenhang stehen. Sie ist die Nachfragefunktion nach Arbeit. Gilt das Gesetz vom abnehmenden Grenzertrag, dann hat sie fallenden Verlauf.

Bei Gültigkeit des Gesetzes von der abnehmenden Grenzproduktivität kann man also erwarten, dass der Einsatz eines Produktionsfaktors steigt, wenn entweder der Produktpreis steigt oder der Faktorpreis sinkt oder die (physische Grenz)Produktivität zunimmt. Es ist keine Frage, dass es im wesentlichen diese Überlegung ist, auf die sich die Forderung nach sinkenden Löhnen zur Verbesserung der Beschäftigungssituation stützt. Dazu kommt natürlich der langfristig einsetzende Substitutionsprozess mit dem Faktor Kapital. Gleichwohl finden sich insbesondere auf der makroökonomischen Argumentationsschiene auch stichhaltige Gegenargumente.

Mit der Kenntnis der Optimalitätsbedingungen für das gewinnmaximierende Güterangebot bzw. den gewinnmaximierenden Faktoreinsatz lassen sich für den Regelfall - für Randlösungen gilt das nicht - folgende Aussagen festhalten:

• Mit steigendem Produktpreis steigt das Güterangebot der Unternehmung.
• Alle Vorgänge, die die Grenzkosten beeinflussen, haben Auswirkungen auf das optimale Angebot. Das sind z.B. technischer Fortschritt, Steuern auf die Produktionsmenge oder den Produktionswert, Änderungen der Preise der variablen Produktionsfaktoren. Fixkostenänderungen oder eine reine Gewinnsteuer haben keinen kurzfristigen Einfluss auf das Angebot.
• Langfristig wird das Angebot auf Güterpreisänderungen elastischer reagieren als kurzfristig.

Nach ähnlichen Seiten im WWW suchen