Diese Seite funktioniert nur mit Javascript.
Die Normative Theorie5.2.1 Scitovsky-IndifferenzkurvenGroße Nutzenmöglichkeitskurve
citovsky-Indifferenzkurven sind Indifferenzkurven für Gruppen von Individuen im Güterraum. Sie zählen damit zur Gruppe gesellschaftlicher Indifferenzkurven, wobei zum Zweck der grafischen Darstellbarkeit die Gesellschaft meist aus nur zwei Individuen besteht.
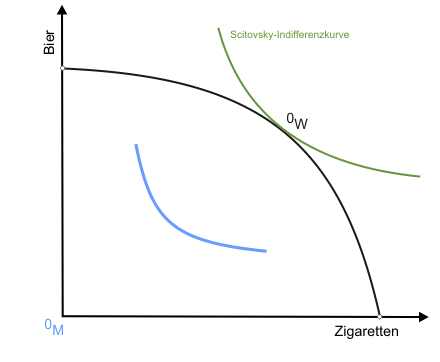
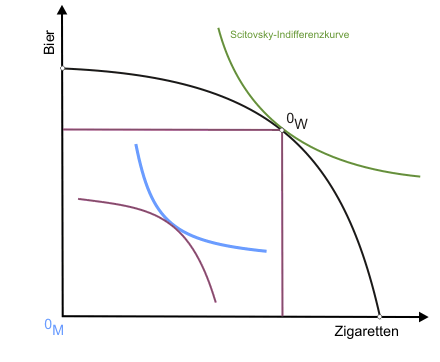
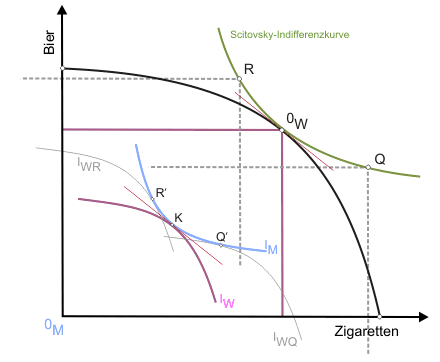
Zur Konstruktion einer Scitovsky-Indifferenzkurve wird Abbildung 1 eingesetzt. Sie zeigt ein Allgemeines Gleichgewicht mit der Übereinstimmung von Grenzrate der Substitution und Grenzrate der Transformation, wie wir es gerade abgeleitet hatten.
Ausgangspunkt der Konstruktion sind die beiden Indifferenzkurven von Konsument und Konsumentin, die sich in K auf der Kontraktkurve tangieren (Bild 9). Für die beiden durch diese individuellen Indifferenzkurven gegebenen Nutzenniveaus sollen jetzt alle Kombinationen von Bier und Zigaretten gefunden werden, die gerade ausreichen, um die Nutzen beider Konsumenten konstant zu halten.
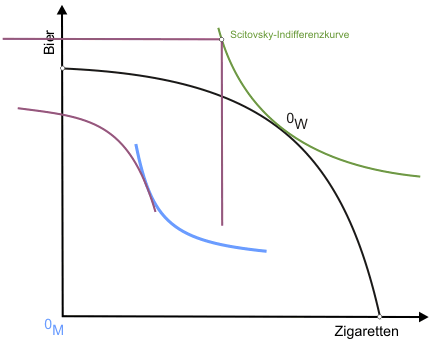
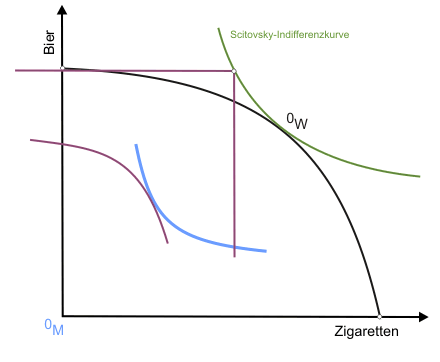
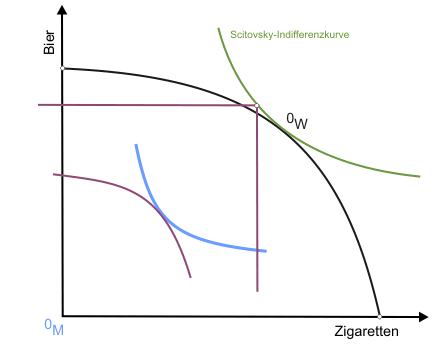
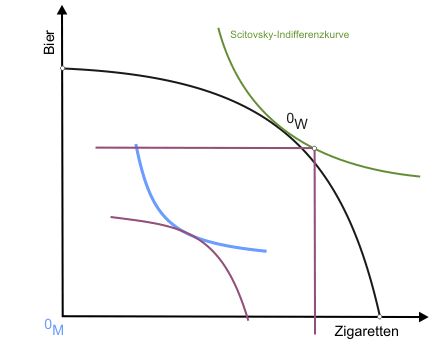
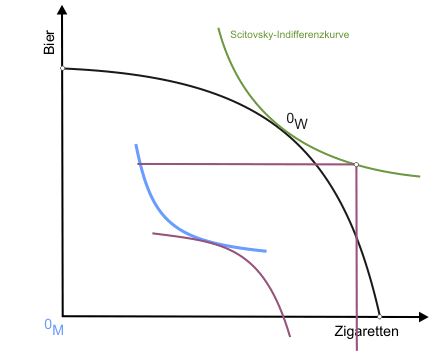
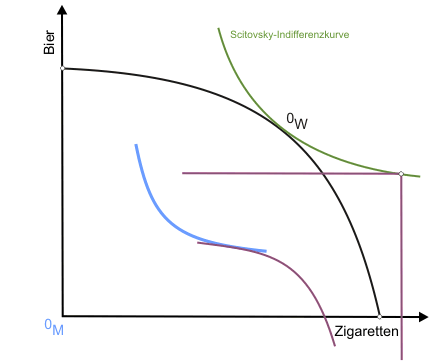
Eine dieser Gütermengenkombinationen ist bereits durch den Punkt OW auf der Transformationskurve bekannt. Um weitere zu finden, lässt man die Indifferenzkurve der Konsumentin an der des Konsumenten entlanggleiten (beide individuellen Nutzen sind dann ex definitione konstant), wobei sich der Ursprung des Indifferenzkurvendiagramms der Konsumentin unter anderem in die in Abbildung 1 eingezeichneten Punkte Q und R verlagert. Folgt man dem Verlauf des Ursprungs während der Verschiebungsaktion (dargestellt in der klickbaren Abbildung), erhält man eine Scitovsky-Indifferenzkurve für die beiden vorgegebenen individuellen Nutzenniveaus.
Da in K die Grenzrate der Substitution gleich der Grenzrate der Transformation war, tangiert die Scitovsky-Indifferenzkurve die Transformationskurve in OW. Das heißt, bei der gegebenen Faktorausstattung ist keine andere Produktion möglich, die einem der beiden Konsumenten einen höheren Nutzen ermöglicht, ohne den anderen zu schädigen (K erfüllt die drei Bedingungen des Allgemeinen Gleichgewichts).
Nun gibt es auf der Kontraktkurve in Abbildung 1 alternative Punkte zu K, die nicht den drei Bedingungen des Allgemeinen Gleichgewichts genügen, für die wir jedoch auch Scitovsky-Indifferenzkurven konstruieren können. Aufgrund der Konstruktionsanweisung verlaufen alle diese Scitovsky-Indifferenzkurven durch OW. Ergo:
Ist die dritte Bedingung des Allgemeinen Gleichgewichts (GRT = GRS) nicht erfüllt, dann schneiden die Scitovsky-Indifferenzkurven die Transformationskurve. Es finden sich dann also unterhalb der Produktionsmöglichkeitengrenze Gütermengenkombinationen, die ausreichen, um beide Konsumenten auf konstantem Nutzenniveau zu halten, so dass eine Verbesserung nach dem Pareto-Kriterium möglich wäre.
Um die nicht ganz leicht einzusehende Konstruktionsweise von Scitovsky-Indifferenzkurven noch etwas zu verdeutlichen, wiederholen wir die Konstruktion in einer etwas formaleren Sprache: Zunächst wählen wir einen beliebigen Punkt P (nicht eigezeichnet - es könnte zum Beispiel Punkt K sein) auf der Kontraktkurve in Abbildung 1 aus. Für diesen Punkt ermitteln wir die beiden zugehörigen Nutzenniveaus UM° und UW° von Konsument und Konsumentin. Jetzt geben wir eine beliebige Zigarettenmenge Z° vor und suchen die zugehörige minimale Menge Bier, die zusammen mit Z° gerade ausreicht, bei effizienter Verteilung Konsument und Konsumentin auf den festgelegten Nutzenniveaus U° zu halten. Indem wir dies für ausreichend viele vorgegebene Zigarettenmengen wiederholen, finden wir als Scitovsky-Indifferenzkurve Bier-Zigarettenmengen-Kombinationen, die gerade ausreichen, UM° und UW° zu sichern.
Das wichtige Ergebnis, dass die Scitovsky-Indifferenzkurven von konvexer Gestalt sind, macht man sich - wie so oft - am einfachsten an einem Spezialfall klar. Stellen wir uns dazu vor, die Indifferenzkurven des Konsumenten hätten die Gestalt fallender Geraden, das hieße seine Grenzrate der Substitution wäre konstant - oder etwas technischer: seine Substituionselastizität wäre unendlich. Wenn wir an dieser geraden Indifferenzkurve (hmmm?!) des Konsumenten die Indifferenzkurve der Konsumentin entlanggleiten lassen, erhalten wir eine "gerade" Scitovsky-Indifferenzkurve. In diesem Fall bleibt der Ausgangspunkt auf der Indifferenzkurve der Konsumentin während der ganzen Verschiebungsaktion der Tangentialpunkt, da ja die Steigungen übereinstimmen müssen und die Steigung der Indifferenzgeraden des Konsumenten wie angenommen konstant ist. Umgekehrt gilt für den Fall einer geraden Indifferenzkurve der Konsumentin und konvexer Indifferenzkurven des Konsumenten, dass der Tangentialpunkt in K in Abbildung 1 (Bild 9) fix ist und der Koordinatenursprung der Konsumentin sich parallel zu ihrer tangierenden Indifferenzkurve auf einer geraden Scitovsky-Indifferenzkurve bewegt. Abgesehen von diesen Extremfällen führt augenscheinlich die Konvexität beider Indifferenzkurven auch zu einer konvexen Scitovsky-Indifferenzkurve.
Man macht sich leicht klar, dass eine höhere Scitovsky-Indifferenzkurve eine Verbesserung der gesellschaftlichen Wohlfahrt (auf diesen Begriff wird später noch genauer eingegangen) anzeigt, die dem Pareto-Kriterium genügt. Dazu muss man sich nur vorstellen, es stünden von beiden Gütern mehr als durch den Punkt OW angezeigte Mengen zur Verfügung. Mit diesem Mehr an Gütern kann man offensichtlich Nutzen eines oder beider Individuen erhöhen - indem einer die gesamten OW übersteigenden Gütermengen erhält oder sie zwischen beiden verteilt werden.
Die Scitovsky-Indifferenzkurve ist also ein Instrument zur Beurteilung der gesellschaftlichen Wohlfahrt, das auf dem paretianischen Werturteil aufgebaut ist. Im Vergleich zu den Überlegungen im Bereich der positiven Theorie führt es jedoch nicht wirklich weiter, da sich die Scitovsky-Indifferenzkurven schneiden können. Bevor wir an dieses Manko im folgenden Gliederungspunkt wieder anknüpfen, haben wir uns noch mit der Großen Nutzenmöglichkeitskurve zu beschäftigen, wobei uns die Scitovsky-Indifferenzkurven einen wichtigen Dienst leisten können.