Diese Seite funktioniert nur mit Javascript.
Einkommens- und Substitutionseffekt2.3.2.1 Exkurs - Intertemporale KonsumentscheidungenExkurs - Kurzfristiges Arbeitsangebot
enn Sie sich bis zu diesem Punkt durchgearbeitet (durchgekämpft?) haben, werden Sie gleich erkennen können, dass sich das behandelte Instrumentarium aus der Theorie des Haushalts auch für weitergehende Fragestellungen gewinnbringend einsetzen lässt. Dieses Erfolgserlebnis werden Sie aber nur haben, wenn Sie sich mit der Budgetgerade, den Indifferenzkurven und der Analyse von Einkommens- und Preisänderungen wirklich vertraut gemacht haben. Sollten Sie nur an den Grundlagen interessiert sein, können Sie diesen Abschnitt überspringen, der eher eine Anwendung denn neue Inhalte vorstellt und von daher den Charakter eines Exkurses hat.
as wollen die Menschen in Deutschland - wie die meisten anderen wohl auch - im Leben eigentlich erreichen? Ein Eigenheim, möglichst Hanglage und Fernblick, alle zwei Jahre ein neues Auto und ein oder zwei Kinder scheinen für die meisten der Schlüssel zum Glück. Diese Konsumwünsche verwirklichen Haushalte in der Regel, indem sie Kredite aufnehmen. Kinder, Autos und ein Haus sind die teuersten Anschaffungen, die sich Familien in ihrem Leben leisten.
Wer sich in seinem Bekannten- und Verwandtenkreis umsieht, wird vielleicht feststellen, dass junge Familien sich diese Wünsche gern schon heute erfüllen würden, obwohl ihnen das notwendige Budget fehlt. Den Umstand, dass man sich einen Wunsch lieber heute als morgen erfüllt, bezeichnet man als Zeitpräferenz. Wer würde nicht, wenn er denn wählen könnte, lieber am nächsten Samstag einen Sechser im Lotto haben als erst in fünf Jahren? Wer würde seine Erkältung nicht lieber heute loswerden als erst in einer Woche? Warum schenken Onkels und Tanten, die auf Besuch kommen, ihren Neffen und Nichten die Mitbringsel, wenn sie ankommen und nicht erst kurz bevor sie sich wieder verabschieden? Genau. Weil sie wissen, dass es einen Wert hat, wenn man ein Gut eher besitzt. Andere Argumente gibt's natürlich auch.
Irgendwo in Deutschland, 15. Nov. Christian ist ein schlaues Kind. Es glaubt nicht mehr an den Weihnachtsmann und weiß, dass seine Eltern die Weihnachtsgeschenke bereits gekauft haben: "Es ist nur vernünftig, wenn ihr mir die Geschenke schon heute gebt. Schließlich habe ich eine positive Zeitpräferenz."
Das muss die sprachlosen Eltern doch überzeugen, oder?
Die Zeitpräferenz lässt sich messen. Sie ist der Betrag, den man gerade so aufzugeben bereit ist, um ein Gut in der gegenwärtigen Periode anstatt erst in der nächsten Periode zu erhalten. Wenn man diesen Betrag zum Wert des Gutes in Beziehung setzt, erhält man die Zeitpräferenzrate. Als Periode ist meist ein Jahr definiert.
Das lässt sich mit einem einfachen Zahlenbeispiel illustrieren: S. hat bei G. eine Schuld in Höhe von 100 Euro, die in einem Jahr fällig wird. G. bietet S. an, er möge heute 95 Euro zahlen. Seine Schuld sei damit getilgt. G. ist somit bereit, 5 Euro aufzugeben, um das "Gut" heute anstatt erst in einem Jahr zu erhalten. Die Zeitpräferenzrate ist damit ungefähr 5%. Ungefähr, da es sinnvoll ist, als Bezugsgröße den Wert in der Gegenwart heranzuziehen. So müssen 95 Euro mit 5,26 % verzinst werden, damit in einem Jahr 100 Euro daraus werden.
Jetzt setzt natürlich sofort folgende Überlegung ein: Wenn G sich bei einer dritten Person D. zu einem niedrigeren Zinssatz Geld leihen könnte, dann würde er S. diesen Vorschlag natürlich nicht unterbreiten.
Dieses Zusammenspiel zwischen den (Markt-)Zinssätzen und der Zeitpräferenzrate wird jetzt etwas systematischer untersucht. Dazu werden die Annahmen des Standardmodells etwas modifiziert:
- Es gibt zwei Perioden, die Gegenwartsperiode und die Zukunftsperiode. In der Gegenwartsperiode findet Gegenwartskonsum $C_0$ statt, in der Zukunftsperiode Zukunftskonsum $C_1$.
- Der Zukunftskonsum unterscheidet sich in seiner Struktur nicht vom Gegenwartskonsum. Eine Einheit dieser Konsumgüter kostet in der Gegenwartsperiode wie in der Zukunftsperiode jeweils $p=1$. Es gibt also Preis(niveau)stabilität, d. h. keine Inflation.
- In beiden Perioden erzielt der Haushalt ein gleich hohes Einkommen $E = E_0 = E_1$. Diese Annahme bewirkt erfahrungsgemäß, dass man das Modell leichter durchdenken kann. Zudem ist der Begriff der Zeitpräferenz für diese Situation definiert. Die Aussagekraft des Modells wird durch diese Annahme in keiner Weise eingeschränkt.
- Habenzinsen $i_H$ und Sollzinsen $i_S$ sind gleich hoch. Etwas eleganter formuliert: "Es wird ein perfekter Kapitalmarkt unterstellt." Darunter wäre nämlich ein vollkommener Markt bei Konkurrenz zu verstehen, der impliziert, dass die Spar- und Kreditzinsen gleich hoch sind, da bei Fehlen jeglicher Transaktionskosten Gewinne aus Geldverleih anfallen würden, wenn die Kredit- über den Sparzinsen lägen.
Der betrachtete Haushalt besitzt Präferenzen, die den üblichen Annahmen genügen sollen, über die beiden Güter, die mithilfe der Nutzenfunktion $U\left(C_0,C_1\right)$ und Indifferenzkurven abgebildet werden.
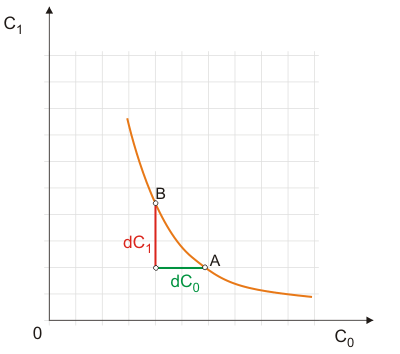
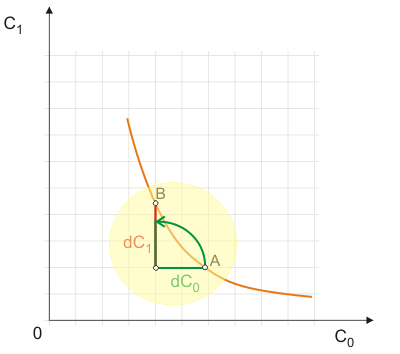
In diesem Aspekt ändert sich gegenüber dem bisher betrachteten zeitgleichen Konsum zweier Güter X und Y eigentlich nichts. Ebenso wie die Indifferenzkurvensteigung die Grenzrate der Substitution zwischen X und Y anzeigte, zeigt sie nun die Grenzrate der Substitution zwischen Gegenwarts- und Zukunftskonsum. Damit spiegelt die Steigung der Indifferenzkurven die Zeitpräferenz des Haushalts wider, denn sie informiert ja, in welchem Verhältnis der Haushalt bei Indifferenz bereit ist, für zukünftigen auf gegenwärtigen Konsum zu verzichten (oder umgekehrt). Aus der maussensitiven Grafik kann man erkennen, dass der Haushalt im Bereich zwischen A und B eine positive Zeitpräferenzrate besitzt (${\rm{d}}{C_1} > {\rm{d}}{C_0}$). Das Gesetz von der abnehmenden Grenzrate der Substitution bedeutet im vorliegenden Kontext einfach, dass die Haushalte ein über die Perioden ausgeglichenes Konsumniveau gegenüber starken Schwankungen im Lebensstandard präferieren.
Bei der Budgetrestriktion kommt es im Vergleich zum Standardmodell zu kleineren Änderungen. Ein möglicher intertemporaler Konsumpunkt lässt sich ohne Weiteres Nachdenken sofort konstruieren: der Haushalt gibt sein Gegenwartseinkommen $E_0$ vollkommen für Gegenwartskonsum $C_0$ und sein Zukunftseinkommen $E_1$ vollkommen für Zukunftskonsum $C_1$ aus (Punkt P in Abb. 2).
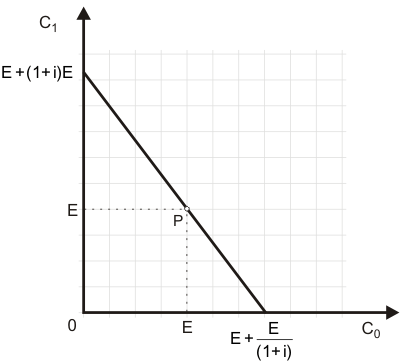
Durch Sparen oder Kreditaufnahme kann der Haushalt Gegenwarts- in Zukunftskonsum transformieren und umgekehrt. Unrealistisch, aber hilfreich, sind die Überlegungen, welche Mengen der Haushalt in der Gegenwart oder in der Zukunft maximal konsumieren könnte, wenn er in einer der beiden Perioden jeweils vollkommen auf Konsum verzichten würde. Angenommen, er verzichtet in der Gegenwart auf Konsum, dann kann er sein Einkommen sparen und hat dann in der Zukunft den Betrag $E + E(1+i)$ zur Verfügung. Umgekehrt könnte er auf Zukunftskonsum verzichten. Da er in der Lage wäre, in der Zukunftsperiode den Betrag E zurückzuzahlen, kann er in der Gegenwart maximal einen Betrag in Höhe von $E/(1+i)$ als Kredit aufnehmen. Also beträgt der maximal mögliche Gegenwartskonsum $E+E/(1+i)$.
Wenn man die beiden maximal möglichen Konsummengen durch eine Gerade verbindet, stellt man zunächst fest, dass P auf dieser Geraden liegt. Außerdem ist es nicht weiter schwierig, die Gleichung dieser Gerade zu bestimmen:
$$C_1 = E + E(1+i) - (1+i)C_0\tag{1}$$Wird diese Gleichung - bei der es sich natürlich um die intertemporale Budgetrestriktion handelt - etwas umgeformt, dann kann man sie sehr schön interpretieren:
$$C_1 - E = (1+i)(E - C_0) \tag{2}$$Auf der linken Gleichungsseite findet man die Differenz zwischen zukünftigem Konsum und zukünftigem Einkommen. Sie muss der verzinsten Differenz zwischen gegenwärtigem Konsum und gegenwärtigem Einkommen entsprechen. Im einfachsten Fall ohne Zinsen ergäbe sich, dass man in der Zukunft genau das mehr konsumieren kann, was man in der Gegenwart an Konsumverzicht geleistet hat.
Wenn $(E-C_0)$ positiv ist, wird der Haushalt Sparer oder Gläubiger genannt, im umgekehrten Fall Kreditnehmer oder Schuldner. Zu welcher Gruppe der Haushalt gerechnet werden muss, hängt nun natürlich vom Zusammenspiel von Zeitpräferenzrate und Marktzins ab.
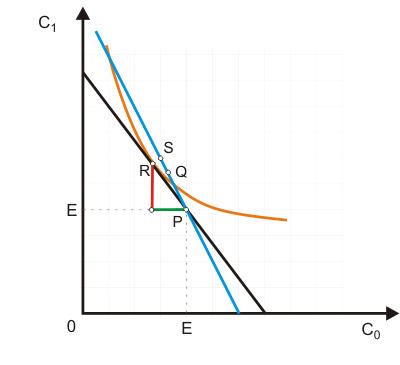
Wie man in Abb. 3 erkennt, die durch Kombination von Abb. 1 und Abb. 2 entstanden ist, handelt es sich bei dem betrachteten Haushalt um einen Kreditnehmer. Um die durch die grüne Strecke angezeigte Gütermenge in der Gegenwart mehr konsumieren zu können (Kreditaufnahme), muss er in der Zukunft auf die durch die rote Strecke angezeigte Gütermenge verzichten (Rückzahlung der Kredites zzgl. Zinsen).
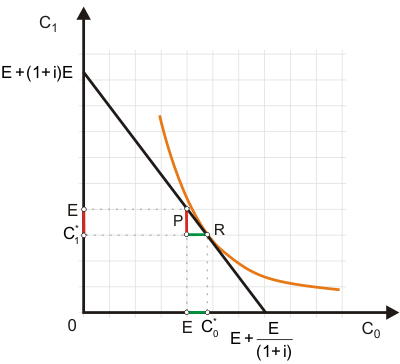
Diese Gleichgewichtsbedingung lässt sich wie im Standardmodell selbstverständlich auch alternativ in Grenznutzenbegriffen formulieren:
$$\cfrac{\cfrac{dU}{dC_0}}{\cfrac{dU}{dC_1}}=\frac{1+i}{1}=\ \ \left[\frac{p_{C_0}}{p_{C_1}}\right]\tag{3}$$Das Verhältnis der Grenznutzen von Gegenwarts- und Zukunftskonsum muss dem Verhältnis der Güterpreise entsprechen. Es zeigt sich also, dass man die notwendige Bedingung für ein Haushaltsgleichgewicht im Standardmodell einfach auf das intertemporale Problem übertragen kann. Man muss dabei nur erkennen, dass das Preisverhältnis zwischen einer Einheit des Zukunftskonsums und einer Einheit des Gegenwartskonsums - also die Steigung der Budgetgeraden - durch $1+i$ gegeben ist. Je höher der Zinssatz ist, desto teurer ist der Konsum in der Gegenwart.
Zwei (komparativ statische) Fragen wollen wir abschließend untersuchen:
Frage 1: Wenn ein Haushalt Sparer ist und der Marktzins steigt, kann er dann zum Kreditnehmer werden?
Frage 2: Wenn das Einkommen in der Gegenwart und in der Zukunft gleich hoch ist, und alle Haushalte eine Präferenz für Gegenwartskonsum haben, kann es dann sein, dass der Marktzins null ist? ...zur Antwort
Antwort auf Frage 1:
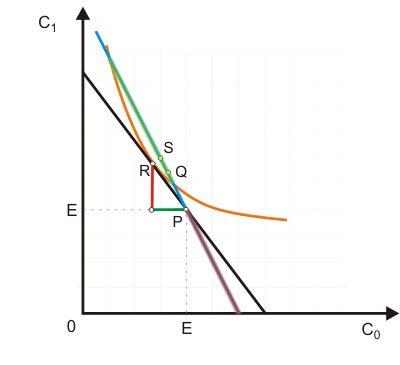
Hier kommen wir mithilfe eines Diagramms, das uns einen Sparer zeigt, schnell zu einer Antwort. Der steigende Zins macht den Zukunftskonsum relativ billiger. Beachten Sie, dass sich im Unterschied zum Standardmodell die Budgetgerade nicht um einen Achsenschnittpunkt, sondern von der schwarzen um den Punkt P im Uhrzeigersinn in die blaue dreht. P selbst ist von der Zinshöhe offensichtlich unbeeinflusst.
Alle intertemporalen Konsumgüterbündel unterhalb der alten Budgetrestriktion hätte der Haushalt auch schon in der Ausgangssituation wählen können. Da er das nicht getan hat, wissen wir, dass diese Bündel in seinen Augen schlechter sind als das Anfangsgleichgewicht R (maussensitive Grafik). Alle Güterbündel, die eine höhere Indifferenzkurve erreichen lassen, liegen in einem Bereich, in dem der Haushalt spart. Dies trifft z. B.. auf die Bündel S und Q zu. Er bleibt also auf jeden Fall Sparer. Allerdings kann es durchaus sein, dass das Sparen abnimmt (was davon abhängig ist, wie elastisch Gegenwarts- und Zukunftskonsum auf das veränderte reale Einkommen reagieren), wie man an Punkt Q erkennen kann. Es ist also nicht sicher, dass eine Erhöhung der Zinsen zu einer Zunahme des Sparens führt. Gesamtwirtschaftlich ist das aber sehr wahrscheinlich, denn bei steigenden Zinsen haben Kreditnehmer einen Anreiz, zu Sparern zu werden, wie man mit einer analogen Überlegung, wie wir sie hier angestellt haben, nachweisen kann.
Angenommen, alle Menschen wären ohne Zeitpräferenz (ihre Zeitpräferenzrate sei null, wenn $C_0$ gleich $C_1$ ist). Infolge technischen Fortschritts liegt das zukünftige Einkommen über dem gegenwärtigen Einkommen. Zeigen Sie, dass ein positiver Zinssatz resultieren muss.
Hinweis: Zeichnen Sie ein Diagramm. Überlegen Sie, wo im Unterschied zu Abb. 2 der Punkt P liegt. Überlegen Sie dann, welches intertemporale Bündel ein Haushalt konsumieren möchte, der keinen Unterschied zwischen gegenwärtigem und zukünftigem Konsum macht. Und überlegen Sie schließlich, ob das für alle Haushalte ein Gleichgewicht sein kann.
Antwort auf Frage 2:
Diese Frage können lässt sich auch ohne die Hilfe eines Diagramms beantworten, denn die Antwort liegt eigentlich auf der Hand. Schließlich wünschen ja alle Haushalte infolge ihrer Zeitpräferenz, in der Gegenwart mehr zu konsumieren, als ihr Einkommen erlaubt. Sie müssen deswegen Kredit aufnehmen. Das kann aber nur klappen, wenn auch Haushalte zu sparen bereit sind. Damit sich zwischen Spar- und Kreditvolumen ein Gleichgewicht einstellt, muss das Sparen durch steigende Zinsen attraktiv werden. Zugleich wird die Kreditaufnahme unattraktiver. Durch die steigenden Zinsen werden einige der Kreditnehmer zu Sparern, so dass sich ein Gleichgewicht einstellen kann.
Nach ähnlichen Seiten im WWW suchen