Diese Seite funktioniert nur mit Javascript.
Exkurs - Intertemporale Konsumentscheidungen2.3.2.2 Exkurs - Kurzfristiges ArbeitsangebotNachfragefunktionen
(Einkommen-Freizeit- oder Konsum-Freizeit-Modell)
ie kann denn das Arbeitsangebot ein Anwendungsbeispiel für Nachfrageentscheidungen eines Haushalts sein? Die Antwort mag überraschen: Es existiert gar keine eigenständige Theorie des Arbeitsangebotes. Wenn dennoch von ihr die Rede ist, dann geht es eigentlich um die "Theorie der Freizeitnachfrage" – auch wenn das kein Mensch so nennt. Und nun ahnen Sie sicherlich auch schon, mit welchem Trick das Arbeitsangebot erklärt wird. Die mikroökonomische Theorie definiert einfach eine zusätzliche Arbeitsstunde als eine verlorene Freizeitstunde. Dann erklärt sie mit ihrem üblichen Instrumentarium die Nachfrage nach Freizeit. Die Zeit, die nicht als Freizeit nachgefragt wird, ist angebotene Arbeitszeit.
Mit drei Symbolen wird sofort deutlich, was gemeint ist. $T$ sei das zur Verfügung stehende Zeitbudget (z. B. 24 Stunden an einem Tag), $A$ sei die Arbeitszeit und $F$ sei die Freizeit. Dann gilt
$$T = A + F\tag{1}$$Da $T$ eine Konstante ist, steht mit der Nachfrage nach Freizeit $F$ die vom Haushalt gewünschte Arbeitszeit $A$ fest. Ob sich dieses Arbeitsangebot dann auch in die Tat umsetzen lässt, steht auf einem anderen Blatt. Hier wird ja zunächst erstmal nur eine Seite des Arbeitsmarktes betrachtet, die Seite der Haushalte, die auf dem Arbeitsmarkt als Anbieter auftreten.
Bevor nun das individuelle Arbeitsangebot genauer analysiert wird, ist noch zu erklären, warum hier von einer kurzfristigen Entscheidung die Rede ist. Man versteht darunter, in welchem Umfang ein Haushalt an einem Tag, in einer Woche, in einem Monat oder einem anderen Zeitraum seine Arbeitskraft anzubieten wünscht. Der Haushalt kann neben dieser quantitativen auch eine qualitative Entscheidung hinsichtlich seines Arbeitsangebotes treffen. Dabei handelt es sich aber typischerweise um langfristige Entscheidungen. So entscheidet der Haushalt z. B. über seine Aus- und Weiterbildung. Entscheidet er sich für eine Berufsausbildung, dann bietet er im Anschluss als Facharbeiter c. p. besser qualifizierte und produktivere Arbeit an als un- oder angelernte Arbeitskräfte. Diese langfristigen Entscheidungen zeichnen sich dadurch aus, dass in der Gegenwart direkte und vor allem indirekte (Ausbildungs)Kosten in Form von entgangenen Einkommen anfallen. In der Zukunft stehen diesen Kosten Erträge in Form höherer Arbeitseinkommen gegenüber. Solche Investitionsentscheidungen, die das Arbeitsangebot eines Haushalts qualitativ verändern, werden im Rahmen der sog. Humankapitaltheorie untersucht.
Zur Ermittlung der Nachfrage nach Freizeit sind nur kleinere Modifikationen an dem Modell vorzunehmen, das bisher zur Ermittlung der Nachfrage nach Gütern eingesetzt wurde. Zunächst lässt sich feststellen, dass Freizeit auch ein Gut ist. Sie stiftet ganz offensichtlich Nutzen (wenn man nicht gerade Langeweile hat –aber wer hat die schon?). Man darf wohl auch ohne große empirische Analyse davon ausgehen, dass es sich bei Freizeit um ein superiores Gut handelt. Indizien dafür sind, dass wir uns mit steigendem Lebensstandard (=Einkommen) mehr Urlaub und kürzere Wochenarbeitszeiten leisten. Stellen Sie sich vor, sie kämen durch eine Schenkung oder einen Gewinn zu einem hohen Vermögen. Würden Sie dann länger arbeiten? Natürlich nicht. Das Gegenteil ist der Fall. Menschen, die uns erzählen, nach einem Sechser im Lotto würden sie genau so weiter arbeiten wie bisher, dürften größte Schwierigkeiten haben, uns zu erklären, warum sie denn dann überhaupt Lotto spielen. Wie immer bestätigen Ausnahmen die Regel.
Damit wir unser mühsam entwickeltes Zwei-Güter-Modell weiter verwenden können, betrachten wir neben Freizeit als zweites Gut den Konsum $C$. Darunter können wir uns ein "Durchschnittsgut" vorstellen, das man für einen Preis $p_C$ von 1 Euro kaufen kann. Wenn wir wie bisher annehmen, dass der Haushalt sein gesamtes Einkommen ausgibt, dann folgt mit diesem kleinen Trick, dass die Menge der Konsumgüter gleich dem Einkommen ist. Deswegen kann in Abb. 1 an der Konsumachse zugleich das Einkommen abgelesen werden.
Die Achse, an der das Gut Freizeit abgetragen wird, endet beim Zeitbudget $T$. Da beide Güter Nutzen $U$ stiften und die üblichen Annahmen weiterhin gelten sollen – formal lässt sich
$$U = U(F, C)\tag{2}$$schreiben – haben die Indifferenzkurven den typischen Verlauf.
Ein kleiner Nachteil dieser Konstruktion soll nicht verschwiegen werden. Wenn Freizeit Nutzen stiftet und Arbeit quasi das Gegenteil von Freizeit ist, dann geht mit Arbeit ein Disnutzen einher. Arbeit verursacht dem Haushalt in diesem Modell also ein Leid. Man ist geneigt, wenn man an so manche Arbeit denkt, das zu akzeptieren. Aber die Arbeitszeit an sich verursacht kein Leid. Genauso wenig, wie die Freizeit an und für sich Nutzen stiftet. Die Zeit ist einfach nur da und der Haushalt teilt sie zwischen Freizeit und Arbeitszeit auf. Der Disnutzen der Arbeit entsteht durch die Arbeitsumstände (z. B.. Anstrengung, fremdbestimmte Tätigkeiten), ebenso wie der Nutzen der Freizeit durch die Aktivitäten entsteht, die in der Freizeit unternommen werden (z. B. durch einen Kinobesuch, durch eine Reise oder für manche Menschen auch durch Sport).
Fortgeschrittene Modelle (Beckers Theorie der Allokation der Zeit) tragen dieser Überlegung Rechnung, ohne gegenüber dem richtig verstandenen Grundmodell, auf das sich die Darstellung hier beschränkt, zu wesentlich neuen Erkenntnissen zu führen. Deswegen halten wir hier zunächst daran fest, dass Arbeit Leid und Freizeit Nutzen verursacht.
Um das Modell zu komplettieren, wird noch eine Budgetrestriktion benötigt. Wie wir wissen, lässt sie sich konstruieren, wenn man die Höhe des Einkommens und die Preise der Güter kennt. Doch was kostet eine Stunde Freizeit? Hat die Zeit überhaupt einen Preis?
Diese Frage ist aus dem Stand gar nicht so einfach zu beantworten. Wenn man sich aber klar macht, dass der Haushalt für den Konsum (annahmegemäß) sein Einkommen ausgibt, findet man den Preis der Freizeit ganz nebenbei. Dazu müssen nur noch zwei neue Symbole eingeführt werden. Der Lohnsatz, den der Haushalt pro Arbeitseinheit (z. B. Arbeitsstunde) erhält sei $w$. Außerdem sei zugelassen, dass der Haushalt über sonstiges Einkommen $V$ verfügt, z. B. Zinseinkünfte aus Vermögen, das auch als Nichtarbeitseinkommen bezeichnet wird.
$$p_CC = wA + V\tag{3}$$Auf der linken Seite in Gleichung (3) stehen die Ausgaben des Haushalts für Konsum, auf der rechten Seite sein Einkommen, das sich aus Lohneinkommen $wA$ und Vermögenseinkommen $V$ zusammensetzt.
Nun wird die Zeitrestriktion aus Gleichung (1) genutzt, um in Gleichung (3) die Arbeitszeit $A$ durch einen entsprechenden Ausdruck der Freizeit $F$ zu ersetzen. Sinn dieser Operation ist natürlich, eine Gleichung zu erzeugen, in der nur noch die Unbekannten $C$ und $F$ vorkommen, die in den Abbildungen an den Achsen abgetragen sind.
$$p_CC = w(T - F) + V\tag{4}$$ $$\underbrace{p_CC}_{\text{Konsumausgaben}}=\underbrace{wF}_{\text{Ausgaben für Freizeit}} - \underbrace{wT+V}_{\text{Volles Einkommen}}\tag{5}$$Gleichung (5) zeigt auf der rechten Seite das sog. "volle Einkommen". Dabei handelt es sich um jenen Betrag, den der Haushalt als Einkommen erzielen würde, wenn er sein gesamtes Zeitbudget Arbeit anböte. Auf der linken Seite in Gleichung (5) kann man erkennen, wofür der Haushalt sein volles Einkommen "ausgibt": entweder für Konsum oder für Freizeit. Mehr Freizeit bedeutet notwendigerweise weniger Konsum.
Der Preis der Freizeit ist offenbar der Lohnsatz $w$. Das ist auch sehr plausibel, denn eine Stunde mehr Freizeit kostet eine Stunde Arbeit und somit gerade einen Stundenlohn. Etwas eleganter kann man formulieren:
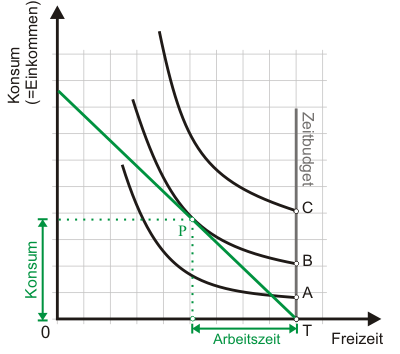
Abb. 2 geht davon aus, dass der Haushalt kein Vermögenseinkommen erzielt. Würde er keine Arbeit anbieten, befände er sich in Punkt $T$. Das gesamte Zeitbudget stünde ihm als Freizeit zur Verfügung, aber er könnte sich keinerlei Konsum leisten. Gleichung (5) kann man in Abb. 2 als grüne Gerade erkennen. Sie stellt seine Budgetrestriktion dar. Würde der Haushalt auf Freizeit verzichten und im Umfang des waggerechten grünen Doppelpfeils Arbeit anbieten, erhielte er ein Einkommen, das ihm einen Konsum im Umfang des senkrechten grünen Doppelpfeils erlauben würde.
Richtig?
Wie längere Arbeitszeiten zu höheren Lohnzahlungen führen, wird in Abb. 2 gezeigt, wenn Sie das Diagramm anklicken. Das "volle Einkommen" oder (auch im Deutschen oft) "full income", das erreicht würde, wenn der Haushalt vollkommen auf Freizeit verzichtete, lässt sich als Achsenabschnitt an der Ordinate ablesen. Ein höherer Lohnsatz $w$ würde die Budgetgerade offensichtlich steiler verlaufen lassen, m.a.W. im Uhrzeigersinn um $T$ drehen.
Das volle Einkommen ist natürlich ein rein hypothetischer Wert. Aber er ist gut für die Überlegung, womit wir die Freizeit, die wir genießen, eigentlich "bezahlen": mit Einkommensverzicht.
Bei der gegebenen Parameterkonstellation befindet sich der Haushalt im Punkt P im Optimum, da die Budgetrestriktion hier die höchste Indifferenzkurve tangiert. Für die analytische Lösung des Problems können wir einfach auf die Überlegungen im Abschnitt Haushaltsoptimum zurückgreifen. Bei der Maximierung des Nutzens (2) unter der Nebenbedingung (5) haben sich gegenüber dem dort betrachteten Problem nämlich nur die Symbole verändert. Wird das zweite Gossensche Gesetz nun nicht auf die Güter $x$ und $y$, sondern auf die Güter Freizeit $F$ und Konsum $C$ angewendet, so ergibt sich
$$\cfrac{\cfrac{\partial U}{\partial F}}{\cfrac{\partial U}{\partial C}}=\frac{w}{p_C} = \left[\text{Reallohn}\right]\tag{6}$$Welcher Aussage stimmen Sie zu?
A. "Freizeit muss man kaufen."
B. "Freizeit gibt's umsonst."
dass das Verhältnis der Grenznutzen von Freizeit und Konsum dem Verhältnis der Preise dieser beiden Güter entsprechen muss, also dem Verhältnis von Lohnsatz und Preis des Konsumgutes. Letzteres ist gerade der Reallohn, den w/p zeigt ja gerade an, wie viele (reale) Gütereinheiten mit dem Lohnsatz gekauft werden können.
Komparative Statik
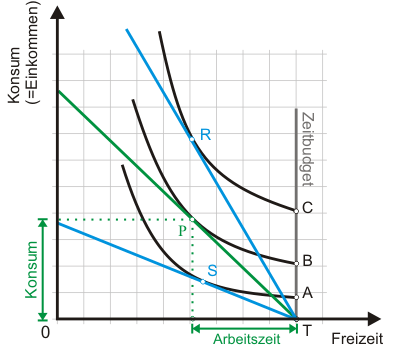
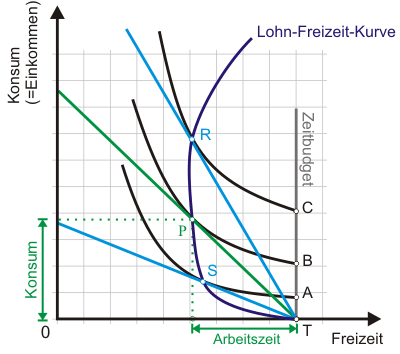
Die Gleichgewichtsbedingung (6) selbst ist recht unspektakulär. Spannender ist die Frage, wie der Haushalt auf Lohnänderungen reagiert. Um dies zu untersuchen, zeigt Abb. 3 im Vergleich zur grünen Ausgangssituation, mit den beiden blauen Budgetgeraden eine Situation mit einem höheren Lohnsatz (blaue Gerade durch R) und eine Situation mit einem geringeren Lohnsatz (durch S). Die Verbindung der Haushaltsoptima bei unterschiedlichen Lohnsätzen ist nichts anderes als eine Preis-Konsum-Kurve, die sichtbar wird, wenn Sie das Diagramm anklicken. Allerdings bezeichnen wir sie hier als Lohn-Freizeit-Kurve.
Die Lohn-Freizeit-Kurve beginnt in T, denn bei einem Lohnsatz von null wird der Haushalt keine Arbeit anbieten. Mit steigendem Lohn geht die Nachfrage nach Freizeit zurück, d.h. das Arbeitsangebot nimmt zu. Allerdings erkennt man, dass mit weiter steigenden Löhnen die Nachfrage nach Freizeit wieder zunimmt, das Arbeitsangebot also bei steigenden Löhnen wider Erwarten rückläufig ist.
Die Erklärung ist im Einkommenseffekt Einkommenseffekt zu finden (s. auch Abb. 5). Der (immer eindeutige) Substitutionseffekt führt bei steigenden Löhnen zu einer Verminderung der Nachfrage nach Freizeit (Gesetz der Nachfrage). Mit steigenden Löhnen steht dem Haushalt aber ein höheres Einkommen zur Verfügung. Der dadurch ausgelöste Einkommenseffekt lässt die Nachfrage nach (der superioren) Freizeit steigen. Der Einkommenseffekt wirkt dem Substitutionseffekt also entgegen und es ist eine empirische Frage, welcher der beiden Effekte die Oberhand gewinnt.
Die Arbeitsangebotsfunktion des Haushalts zeigt also zunächst einen ganz normal ansteigenden Verlauf. Bei hohen Löhnen ist aber nicht auszuschließen, dass sich die Funktion dann durch den immer stärkeren Einfluss gewinnenden Einkommenseffekt rückwärts neigt ("backward bending labor supply curve").
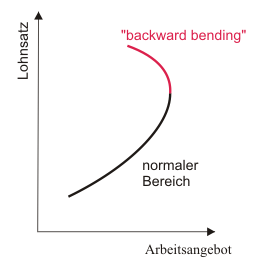
Man macht sich das auch leicht intuitiv klar. Dazu muss man sich nur vorstellen, wie man reagieren würde, wenn der eigene Stundenlohn steigen und steigen und steigen würde. Man bräuchte ja auch Zeit, das hohe Einkommen auszugeben. Das eine einzelne Person bei extrem hohen Stundenlöhnen also wenig Arbeit anbieten wollte, wäre nicht unwahrscheinlich.
Makroökonomisch kann dieser Effekt (zumindest auf auf kurze Sicht) allerdings nicht auftreten. Denn makroökonomisch bleibt der Einkommenseffekt aus. Angenommen der Staat möchte durch sinkende Steuern auf die Einkommen die Menschen bewegen, ihr Arbeitsangebot auszudehnen. Die steigenden Löhne würden infolge des Substitutionseffektes das Arbeitsangebot steigen lassen, denn Freizeit verteuert sich. Die Steuersenkung führt aber zu verminderten Staatseinnahmen, die durch die Erhöhung anderer Steuern (Verbrauchssteuern) oder die Verminderung der Staatsausgaben (z. B.. Transferzahlungen) ausgeglichen werden. Trotz der gestiegenen Stundenlöhne verfügen die Haushalte im Schnitt nicht über höhere Einkommen. Der Einkommenseffekt bleibt somit aus.
Selbst wenn ein Einkommenseffekt einsetzen würde, wäre noch zu bedenken, dass er nur bei denen wirken kann, die bereits in Beschäftigung sind. Höhere Löhne würden aber auch Menschen, die bisher keine Arbeit angeboten haben, in den Arbeitsmarkt locken (z. B. Hausfrauen und trotz quantitaiver Bedeutungslosigkeit, aber wegen der political correctness, auch Hausmänner).
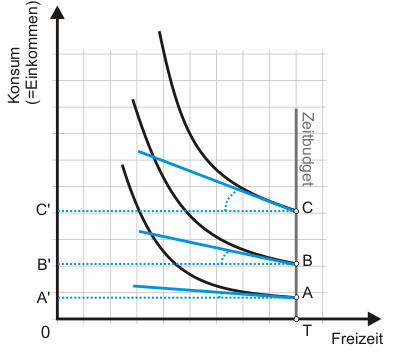
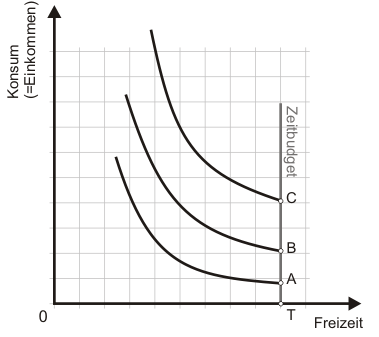
Betrachten wir dazu Abb. 4. Die Punkte A, B und C zeigen an, dass der Haushalt konsumieren kann, ohne dass er Arbeit anbietet. Das bedeutet, er verfügt über Vermögenseinkommen: in A über ein geringes, in B über ein mittleres und in C über das höchste der drei dargestellten Situationen. Die angedeuteten Budgetgeraden sind so konstruiert, dass ein Tangentialpunkt mit den Indifferenzkurven gerade in A, B oder C zustande käme. Die Steigungen der Budgetgeraden zeigen damit die sog. Reservationslöhne (s.a. Reservationspreise ). Erst wenn der Haushalt höhere Löhne erzielen könnte, würde er als Arbeitsanbieter auftreten, da dann ein Tangentialpunkt mit einer Indifferenzkurve links vom Zeitbudget T zustande käme.
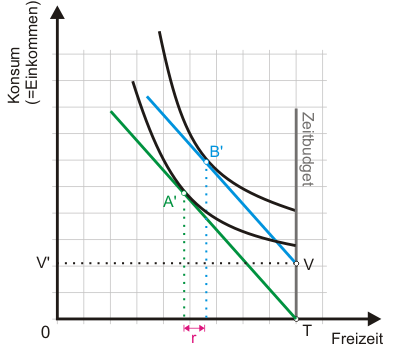
Abschließend zeigt Abb. 5, wie sich eine Änderung des Vermögens auswirkt, die zu Nichtarbeitseinkommen in Höhe TV führt und z. B. aus einem hohen Gewinn, einer Erbschaft oder auch staatlichen Transfers resultieren könnte. Da wir davon ausgehen, dass Freizeit superior ist, muss das Arbeitsangebot sinken. Bei vergleichsweise geringen Löhnen ist nicht auszuschließen, dass der Haushalt sein Arbeitsangebot vollkommen einstellt. Wie Abb. 4 zeigt, steigen die Reservationslohnsätze mit dem Nichtarbeitseinkommen.
Ein Zahlenbeispiel
Der Student S. hat bezüglich Konsum $x$ und Studieren $s$ folgende (Cobb-Douglas-)Nutzenfunktion: $U=x^{1/3}s^{2/3}$. S. bekommt monatlich eine finanzielle Zuwendung von seinen Eltern. Diese Zuwendung entspricht der Summe $m$ am Tag. Aber zum Feiern seiner vielen Partys reicht ihm diese Summe nicht, sodass er zusätzlich noch in einer Birkenfelder Kneipe bedient, wo er einen Stundenlohn $w$ erhält. Diesen Lohn und die Zuwendung gibt S. jeden Monat komplett aus. Der Preis für Konsum ist $p$ (pro Einheit $x$). Täglich braucht er $9$
Stunden, um sich vom Arbeiten und Studieren zu erholen. So verfügt er also über $T$ Stunden ($T=15$), die er zwischen Studieren $s$ und Arbeiten $j$ aufteilt.
Bestimmen Sie die optimale Studierzeit $s^*$ für Student S., wenn $w=10$, $p=1$ und $m = 30$ gilt!
Das Beispiel ist mit kleinen Änderungen aus dem Internet übernommen. Der unbekannte Autor unterrichtet wahrscheinlich an der FH Trier (Standort Birkenfeld).
Wenn die Aufgabe schwierig erscheint, dann wahrscheinlich weil die Symbolik gewöhnungsbedürftig ist. Das Konsumgut $x$ nimmt den Platz von $C$ ein, die Studierzeit $s$ übernimmt die Rolle der Freizeit $F$ und $j$ ist hier die Arbeitszeit. Die Zuwendung der Eltern $m$ ist Vermögenseinkommen.
Damit ergibt sich die folgende Budgetrestriktion: $$px=wj+m$$ Mit dem zweiten Gossenschen Gesetz findet man $$\cfrac{\cfrac{\partial U}{\partial x}}{\cfrac{\partial U}{\partial s}}=\frac{p}{w} \Rightarrow \frac{1s}{2x}=\frac{1}{10} \Rightarrow x=5s$$ Setzt man die Parameterwerte in die Budgetrestriktion ein $$x=10\cdot(15-s)+30$$ und nutzt dieses Resultat, ergibt sich die optimale Studierzeit $s^* = 12$.S. wird also drei Stunden jobben und zwölf Stunden studieren. Die Richtigkeit dieses Resultats kann man überprüfen, indem man berechnet, wie viele Einheiten $x$ S. konsumieren wird und ob sein Einkommen genau den Ausgaben für $x$ entspricht.
Wenn man für die Zuwendung der Eltern (das Vermögenseinkommen) keinen Wert einsetzt, kann man die Studierzeit zu $$s^*=10+\frac{1}{15}m$$ berechnen. Sollte das bei Ihnen ähnlich sein, können Sie sich diese Überlegung vielleicht zunutze machen, indem Sie ihren Eltern erklären, dass Studierzeit für Sie ein superiores Gut ist.
"Der Gewinner und seine 52 Jahre alte Ehefrau entschieden, zunächst eine Rücklage für die Ausbildung der Kinder zu bilden. Außerdem wolle der Mann seinen Arbeitsplatz kündigen, um Arbeitssuchenden Platz zu machen. Ein Jugendtraum solle mit einem Motorboot auf dem Rhein erfüllt werden. Zudem wolle das Paar viel wandern."
Nach ähnlichen Seiten im WWW suchen