Diese Seite funktioniert nur mit Javascript.
Gesetz der Nachfrage I2.1.1 Die BudgetgeradeOffenbarte Präferenzen
Es wird ein Haushalt betrachtet, der sein Einkommen $E$ für die beiden Güter $X$ und $Y$ ausgibt. Das Gut $X$ kostet je Einheit $p_x$, $Y$ kostet je Einheit $p_y$. Welche Gütermengen $x$ und $y$ kann der Haushalt mit seinem Einkommen erwerben?
Es wird ein Haushalt betrachtet, der sein Einkommen in Höhe von 1000 für die beiden Güter $X$ und $Y$ ausgibt. Das Gut $X$ kostet je Einheit 5 , $Y$ kostet je Einheit 4 . Welche Gütermengen $x$ und $y$ kann der Haushalt mit seinem Einkommen erwerben?
Wenn der Haushalt sein gesamtes Einkommen für $X$ verausgabt, kann er $x^{max} = \frac{E}{p_x}$ Einheiten $X$ kaufen.
Wenn der Haushalt sein gesamtes Einkommen für $X$ verausgabt, kann er $200 = \frac{1.000}{5}$ Einheiten $X$ kaufen.
Wenn der Haushalt sein gesamtes Einkommen für $Y$ verausgabt, kann er $y^{max} = \frac{E}{p_y}$ Einheiten Y kaufen.
Wenn der Haushalt sein gesamtes Einkommen für Y verausgabt, kann er $250 = \frac{1.000}{4}$ Einheiten $Y$ kaufen.
Die Ausgaben $A_x$ für Gut $X$ betragen $p_x \cdot x$. Die Ausgaben $A_y$ für Gut $Y$ betragen $p_y \cdot y$. Wenn der Haushalt sein gesamtes Einkommen für die beiden Güter ausgibt, muss die Summe der Ausgaben gleich dem Einkommen sein:
$A_x + A_y = \\ p_x \cdot x + p_y \cdot y = E \tag{1}$Die Ausgaben $A_x$ für Gut $X$ betragen $5x$. Die Ausgaben $A_y$ für Gut $Y$ betragen $4y$. Wenn der Haushalt sein gesamtes Einkommen für die beiden Güter ausgibt, muss die Summe der Ausgaben gleich dem Einkommen sein:
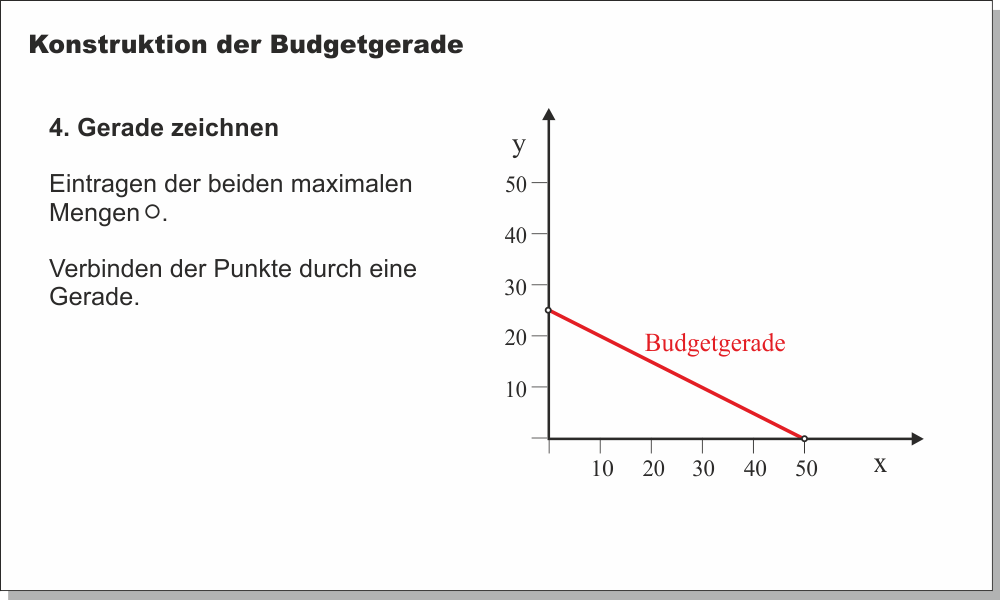
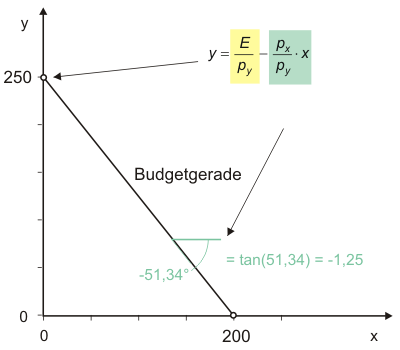
$5x + 4y = 1.000 \tag{1}$Gleichung [1] heißt Budgetgerade. Sie lässt sich grafisch im Güterdiagramm (Abb. 1, Abb. 2) darstellen, an dessen Achsen die Gütermengen $x$ und $y$ abgetragen werden. Um die Budgetgerade einzeichnen zu können, wird Gleichung [1] nach y aufgelöst:*
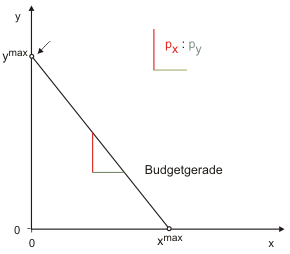
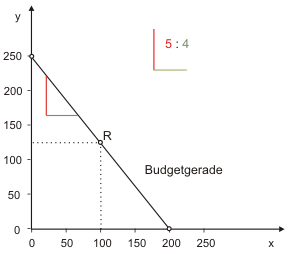
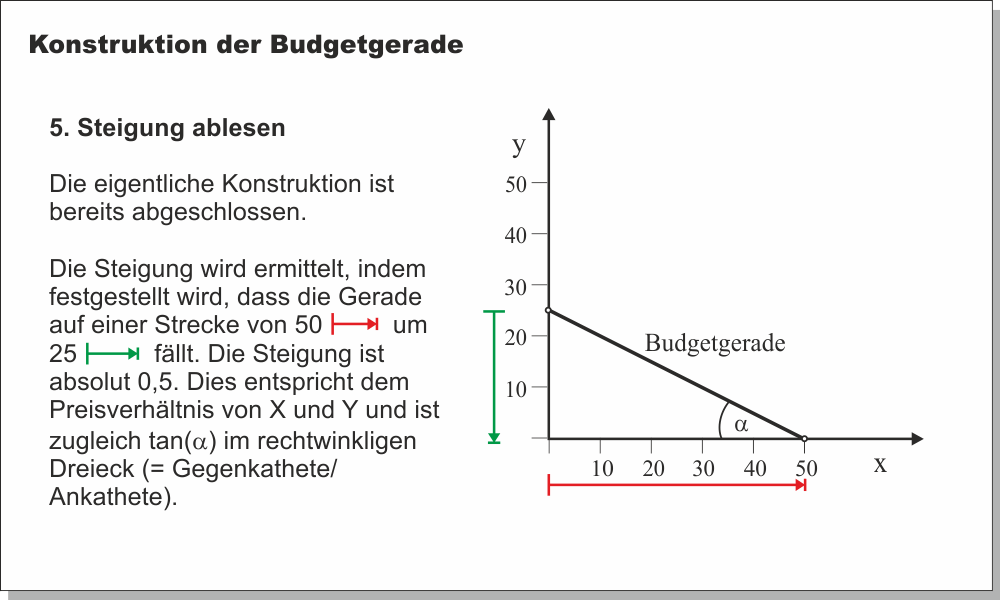
Die (absolute) Steigung der Budgetgerade entspricht dem Preisverhältnis der beiden Güter. Jeder Punkt auf der Budgetgerade zeigt ein Güterbündel, das sich der Haushalt von seinem Einkommen kaufen kann. Da unterstellt wird, dass der Haushalt sein Einkommen vollständig ausgibt, muss er sich auf der Budgetgerade befinden.
Würde abweichend angenommen, das Einkommen $E$ sei die maximal für Konsumausgaben zur Verfgung stehende Summe, dann ließe sich anstelle der Budgetgerade eine Budgetrestriktion formulieren:
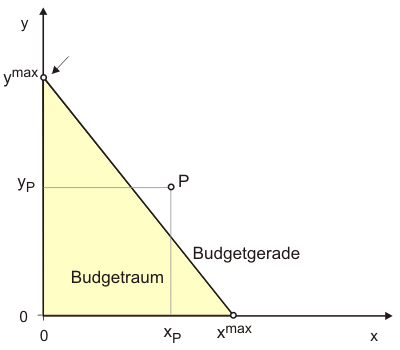
$$A_x + A_y = p_x \cdot x + p_y \cdot y \leq E \tag{3}$$Auf der Budgetgerade wäre die Gleichung erfüllt, unterhalb der Budgetgerade liegen Güterbündel für die der Haushalt sein Einkommen nicht vollständig ausgeben müsste. Die gelbe Fläche in Abb. 3 mit ihrem Rand zeigt den Budgetraum. Er enthält alle Güterbündel, die sich der Haushalt mit seinem Einkommen leisten könnte. Güterbündel außerhalb des Budgetraumes wie P, das die Mengen $x_P$ und $y_P$ enthält, sind bei gegebenem Einkommen und gegebenen Preisen für den Haushalt nicht erreichbar.
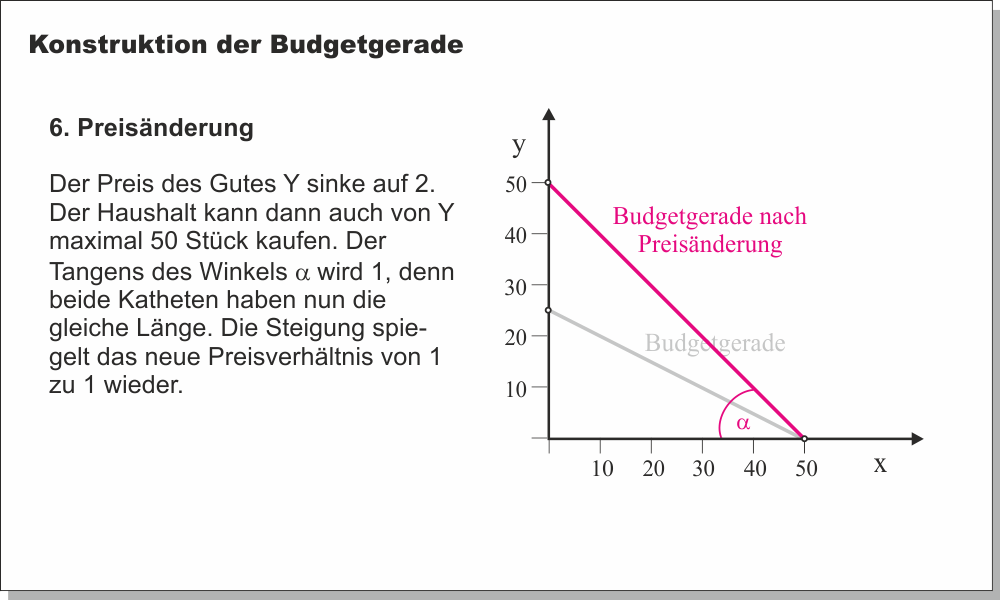
Die Lage der Budgetgerade verändert sich, wenn sich das Einkommen oder einer der Preise verändert:
-
Wenn ceteris paribus das Einkommen steigt, kann sich der Haushalt von beiden Gütern mehr leisten. Die Achsenabschnitte der Budgetgerade wandern nach außen. Da sich die Preise nicht verändert haben, bleibt die Steigung der Budgetgerade gleich. Eine Einkommenssteigerung führt somit zu einer parallelen Verschiebung der Budgetgerade nach außen. Entsprechend verschiebt eine Einkommensminderung die Budgetgerade nach innen.
-
Wenn der Preis des Gutes $X$ steigt, kann sich der Haushalt bei gleichem Einkommen weniger von Gut $X$ leisten. Der Achsenabschnitt $x^{max}$ in Abb. 1 wandert also in Richtung Ursprung. Der Budgetraum verkleinert sich. Die Menge $y^{max}$ ist nicht betroffen, denn sie wird ausschließlich durch das Einkommen und den Preis des Gutes $Y$ bestimmt. Die Steigung der Budgetgerade zeigt, auf welche Menge des einen Gutes der Haushalt verzichten muss, um sich eine (weitere) Einheit des anderen Gutes kaufen zu können. Die Steigung entspricht somit den Opportunitätskosten der Güter. Im Zahlenbeispiel zeigt der Wert 1,25 an, dass der Verzicht auf eine Einheit des Gutes $X$ den zusätzlichen Konsum von 1,25 Einheiten $Y$ ermöglicht.
Die Budgetgerade wird ausschließlich durch reale Größen beeinflusst. Wenn man die Geldeinheiten 2 zu 1 umrechnet, beträgt im Zahlenbeispiel das Einkommen des Haushalts 500 (statt 1000), das Gut X kostet dann 2,50 (statt 5,00) und Y kostet 2 (statt 4). Die Budgetrestriktion ändert sich dadurch nicht, denn die Währungseinheit kürzt sich heraus.
Man sagt auch, der Haushalt ist "frei von Geldillusion". Er lässt sich durch die absolute (nominale) Höhe des Einkommens und der Preise nicht täuschen.

Skizzieren Sie eine Budgetgerade für die beiden Güter. Stellen Sie die beworbene Änderung des Konsums unter der Annahme dar, dass der Stromverbrauch konstant bleibt.