Ineffizienz und Wohlfahrtsverlust

4.2.1.5 Messung der Monopolmacht

Messung der Anbieterkonzentration

ur Messung der Monopolmacht wird der Abstand von Monopolpreis p_M und Konkurrenzpreis p_K herangezogen. Je weiter der Monopolist den Monopol- über den Konkurrenzpreis anhebt, umso stärker soll seine Monopolmacht eingeschätzt werden. Wenn der vom Monopolisten geforderte Preis sich nicht vom Konkurrenzpreis unterscheidet, besitzt das Monopol keine Macht. 

Der einfache Abstand $p_M - p-K$ hat den Nachteil, beliebige Werte annehmen zu können. Wenn man den relativen Abstand misst, normiert man das Maß auf das Intervall $[0,1]$. In dieser Form ist es als Lerners Monopolgrad oder "Lerner's Ratio" bekannt: $$ \text{LR} = \cfrac{p_M - p_K}{p_M} \tag{1} $$

Wenn tatsächlich ein Monopol vorliegt, dessen Macht gemessen werden soll, ist der Konkurrenzpreis aber nicht bekannt. Vielleicht hat man großes Glück und findet für den gleichen Markt in einem Land einen Konkurrenzmarkt vor, der die Beobachtung des Konkurrenzpreises zuließe. Das dürfte aber eher unwahrscheinlich sein. Und außerdem gäbe es dann mit hoher Wahrscheinlichkeit noch weitere Unterschiede, z.B. im Nachfrageverhalten, die das Ergebnis verfälschen würden.

Die Theorie hilft aber weiter: Wäre der Markt ein Konkurrenzmarkt, dann würden sich die Anbieter nach der Preis-Grenzkosten-Regel richten. Daher lässt sich der Preis  in Gleichung [1], zu dem Konkurrenten die Monopolmenge anbieten würden, durch den Wert Grenzkosten ersetzen, der der Regel zufolge ja dem Preis gleich sein muss:

$$ \text{LR} = \cfrac{p_M - C'}{p_M} \tag{2} $$

Der Monopolist hält sich an die Grenzumsatz-Grenzkosten-Regel. Somit kann man die Grenzkosten durch den Grenzumsatz ersetzen, der durch die Amoroso-Robinson-Relation gegeben wird:

$$ \text{LR} = \cfrac{p_M - U'}{p_M} \tag{3} $$ $$ \text{LR} = \cfrac{p_M - p_M(1+\cfrac{1}{E_{x,p}})}{p_M} = -\cfrac{1}{E_{x,p}} \tag{4} $$

Die Vereinfachung des Ausdrucks (nachdem man $p_M$ gekürzt hat) zeigt, dass Lerners Monopolgrad dem (negativen) umgekehrten Wert der direkten Preiselastizität der Nachfrage $E_{x,p}$ entspricht.

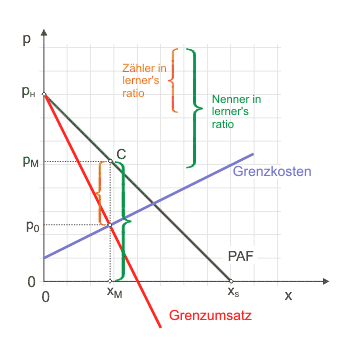
Dieses Ergebnis ist ausgesprochen plausibel, zeigt doch die Preiselastizität an, wie dringlich die Konsumenten auf das Produkt angewiesen sind. Ein absolut kleiner Wert deutet auf einen dringlichen Bedarf hin. In diesem Fall kann der Monopolist einen hohen Preis durchsetzen, ohne dass die nachfragte Menge allzu stark zurückgeht. Mit steigendem Elastizitätswert schwindet die Macht des Monopolisten. Wenn die Nachfrage unendlich elastisch wird, ist gar keine Monopolmacht mehr vorhanden. Das beschreibt aber auch gerade den Verlauf von solchen Preis-Absatz-Funktionen, denen sich Anbieter bei vollkommener Konkurrenz gegenübersehen. 

Nach ähnlichen Seiten im WWW suchen