Diese Seite funktioniert nur mit Javascript.
Das Cournotsche n-pol4.2.2.3 Modell von StackelbergModell von Bertrand
as Oligopolmodell von Heinrich von Stackelberg setzt an einem der zentralen Kritikpunkte des Cournot-Modells an. Die Annahme, beide Duopolisten seien nicht lernfähig, wird für einen der beiden aufgegeben. Die Ausgangssituation des Cournot-Modells wird zwar im Großen und Ganzen beibehalten, dennoch führt die Veränderung der Verhaltensannahme für einen der beiden Anbieter nicht nur zu einer anderen Lösung, sondern zeigt zugleich, wie sich strategische Überlegungen modelltheoretisch erfassen lassen. Das ist - wenn Sie mich fragen - das eigentlich "Schöne" am Stackelberg-Modell.
Schritt für Schritt: Wir betrachten weiterhin ein Mineralwasserduopol und unterstellen sequenzielle Entscheidungen der beiden Duopolisten. Zunächst sei nur Anbieter 1 am Markt. Als Monopolist bietet er die halbe Sättigungsmenge an, um seinen Gewinn zu maximieren. Diese Situation ist in Abbildung 1 mit roten Linien dargestellt. In der Abbildung sind sowohl die Sättigungsmenge als auch der Prohibitivpreis auf 1 normiert. Das ermöglicht ein einfaches und schnelles Berechnen des Umsatzes, der im Mineralwasserfall mit dem Gewinn übereinstimmt.
Wie im Cournot-Modell entdeckt der zweite Anbieter eine Mineralwasserquelle und bringt ein Angebot in Höhe der Hälfte der noch verbliebenen Menge auf den Markt. Anbieter 2 bietet also nach der Cournotschen Verhaltensannahme ¼ an. Das Angebot beider zusammen macht damit ¾ der Sättigungsmenge aus. Der Preis stellt sich deswegen auf ¼ ein. Der Gewinn, der in dieser Situation von Anbieter 1 erzielt wird, ist im klickbaren Diagramm als Fläche dargestellt.
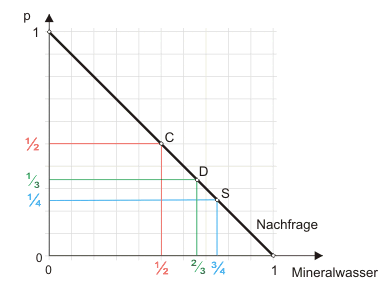
Gewinn von Anbieter 1, wenn er bei der Monopolmenge bleibt (Stackelberg-Führer)
Gewinn von Anbieter 1 in der Zwei-Drittel-Lösung (Cournot)
Vergleich der Situationen (die rote Fläche ginge verloren, die grüne käme hinzu, wenn Anbieter 1 sich auf das Cournot-Spiel einließe)
Jetzt haben wir das Glück, Anbieter 1 bei einem Selbstgespräch belauschen zu können: "Wenn ich mich auf das Cournot-Spiel einlasse, dann landen wir in der Zwei-Drittel-Lösung. Ich würde dann ein Drittel anbieten, und da der Preis ein Drittel wäre, wäre mein Gewinn ein Neuntel. Im Moment aber beträgt mein Gewinn ein Achtel. Und auch wenn einige anderer Ansicht sind: Ein Achtel ist mehr als ein Neuntel. Da bleibe ich doch einfach bei der Monopolmenge und mache mich nicht von den Entscheidungen meines Konkurrenten abhängig." Anbieter 1 erkennt also, dass er momentan mehr Gewinn erzielt, als er erzielen würde, wenn er der Cournotschen Verhaltensannahme folgen würde. Deswegen bleibt er bei der Monopolmenge und begibt sich damit in die sog. Unabhängigkeitsposition.
Seine Entscheidung über die Angebotsmenge ist von der seines Konkurrenten unabhängig. Deswegen wird er auch Mengenführer genannt. Umgekehrt folgt hingegen der Konkurrent den Entscheidungen des Mengenführers. Er befindet sich in einer Abhängigkeitsposition und wird Mengenfolger oder Stackelberg-Folger genannt.
Wir wissen nun, dass sich für Anbieter 1 eine bessere Situation als in der Cournotschen Zwei-Drittel-Lösung erreichen lässt, wenn er einfach stur weiterhin die Monopolmenge anbietet. Aber ist das auch die beste Situation überhaupt, wenn für den anderen Anbieter die Cournotsche Verhaltensannahme gilt?
Sie ist es tatsächlich. Aber mir ist kein Argument bekannt, das dies auf der Ebene lockerer Denkzusammenhänge beweisen könnte. Hier kommt man ohne Zuhilfenahme der Differenzialrechnung nicht weiter.
Dazu verwenden wir Reaktionsfunktionen, die wir aus unseren Überlegungen zum Cournot-Modell kennen. Wenn die Nachfrage nach Mineralwasser durch
$$ p = a - b\left( {{x_1} + {x_2}} \right) \tag{1} $$gegeben ist, kann man die Umsatz- bzw. Gewinnfunktion für Unternehmer 1 als
$$ {U_1} = {G_1} = a{x_1} - bx_1^2 - b{x_2}{x_1} \tag{2} $$schreiben.
Analog beträgt der Gewinn von Anbieter 2
$$ {U_2} = {G_2} = a{x_2} - bx_2^2 - b{x_1}{x_2} \tag{3} $$Nullsetzen der ersten Ableitung
$$ \cfrac{{d{G_2}}}{{d{x_2}}} = a - 2bx_2^{} - b{x_1}\mathop = \limits^! 0 \tag{4} $$liefert die Reaktionsfunktion von Anbieter 2: Für gegebene Mengen $x_1$, die der Mengenführer auf den Markt bringt, informiert diese Funktion den Anbieter in der Abhängigkeitsposition, mit welcher Menge er folgen muss, um seinen eigenen Gewinn zu maximieren:
$$ 2bx_2^{} = a - b{x_1} \space \space \space \Rightarrow \space \space \space {x_2} = \cfrac{1}{2}\cfrac{a}{b} - \cfrac{1}{2}{x_1} \tag{5} $$Das erkennt Anbieter 1. Er weiß, Anbieter 2 wird sich nach seiner Reaktionsfunktion richten. Damit ist für Anbieter 1 aber klar, dass er mit seinen Entscheidungen die Menge von Anbieter 2 steuern kann. Der Umsatz von Anbieter 1 wird von den Entscheidungen, die Anbieter 2 trifft, unabhängig! Formal erkennt man das daran, dass man in der Umsatzfunktion (2) von Anbieter 1 die Menge von Anbieter 2 durch die Reaktionsfunktion (5) von Anbieter 2 ersetzt, was zur Folge hat, dass der Umsatz von Anbieter 1 ausschließlich von der Mengenentscheidung von Anbieter 1 abhängt:
$$ {G_1} = a{x_1} - bx_1^2 - b{x_1} \cdot {x_2} = a{x_1} - bx_1^2 - b{x_1} \cdot \left[ {\cfrac{1}{2}\cfrac{a}{b} - \cfrac{1}{2}{x_1}} \right] \tag{6} $$Jetzt ist nur noch das Maximum dieser Funktion in Abhängigkeit von $x_1$ zu bestimmen. Differenzieren und Auflösen nach $x_1$ liefert nach einigen Vereinfachungsschritten* $$ {x_1} = \cfrac{1}{2}\cfrac{a}{b} \tag{7} $$
Das ist aber gerade die halbe Sättigungsmenge. Also ist es für den ("schlauen") Mengenführer, der das Verhalten des ("dummen") Mengenfolgers bei eigenen Entscheidungen berücksichtigt, gewinnmaximierend, die Monopolmenge anzubieten. Da die Anbieter im Gleichgewicht unterschiedliche Mengen anbieten, wird gelegentlich auch von der Stackelbergschen Asymmetrielösung gesprochen.
Aus der Sicht der Konsumenten ist die Stackelberg-Lösung angenehmer als die Cournotsche Zwei-Drittel-Lösung, da das Mineralwasser zu einem geringeren Preis angeboten wird. Auch aus wohlfahrtstheoretischer Sicht ist die Lösung vorzuziehen.
Welcher Preis würde sich einstellen, wenn beide Duopolisten zugleich die Unabhängigkeitsposition einnehmen würden? Bei welcher anderen Marktform käme genau dieser Preis zustande?
Wie im Cournot-Modell ist die Stabilität der Lösung im Stackelberg-Modell fraglich. Es ist ungeklärt, wer sich in die Unabhängigkeitsposition begibt - zumindest wenn sich die beiden Anbieter nicht durch unterschiedliche Kostenfunktionen, sprich Produktionstechnik, unterscheiden. Warum kommen nicht beide zugleich auf diese schlaue Idee? Wenn dem so wäre, würde sich aber eine vollkommen instabile Situation einstellen (s. Kasten für eine entsprechende Verständnisfrage). Warum verhandeln die Anbieter nicht miteinander, um diese für beide sehr unglückliche Situation zu vermeiden?
Wenn ein Anbieter Kostenvorteile in der Produktion hätte, wäre zwar die Frage einfach zu beantworten, wer die Unabhängigkeitsposition anstrebt. Aber zugleich würde sich natürlich die Frage stellen, warum es nicht zu einem Verdrängungswettbewerb käme. Das Stackelbergsche Gleichgewicht steht also wohl eher auf wackeligen Füßen. Aber es ist ausgesprochen lehrreich. Es zeigt uns, wie wir in einem mikroökonomischen Modell strategisches Verhalten berücksichtigen können.
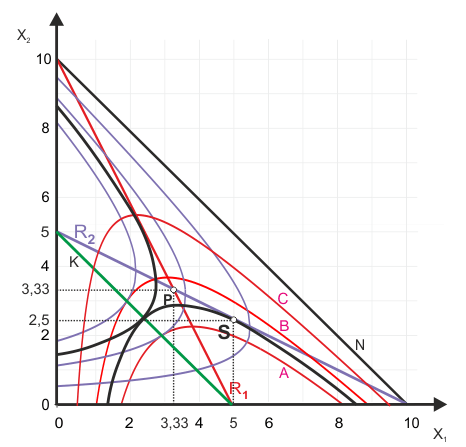
Wenn Sie sich mit dem Konzept der Isoprofitkurve vertraut gemacht haben, können Sie in Abbildung 2 das Stackelbergsche Gleichgewicht auch grafisch erkennen. Die Nachfragefunktion, für die das maßstabsgetreuen Diagramm konstruiert ist, lautet $p = 10 - (x_1 + x_2)$.
Die roten Kurven sind Isogewinnkurven für Anbieter 1, die lilafarbenen Kurven die für Anbieter 2. Die beiden Reaktionsfunktionen schneiden sich im Cournot-Nash-Gleichgewicht P. Auf der grünen Linie K liegen die Kartelllösungen, bei denen ein Anbieter seinen Gewinn nur auf Kosten des anderen erhöhen kann.
Wenn Anbieter 1 der Stackelberg-Führer ist, weiß er, dass Anbieter 2 als Folger einen Punkt auf seiner lilafarbenen Reaktionsfunktion R2 anstreben wird. Also wird Anbieter 1 jene Menge produzieren, mit der er die grafisch gesehen niedrigste Isogewinnkurve erreicht - unter der Nebenbedingung, dass es sich zugleich um einen Punkt auf R2 handelt. Das ist in Punkt S der Fall, wo die Reaktionsfunktion eine Isogewinnkurve tangiert.
Hierbei handelt es sich aber gerade um jene Isogewinnkurve, auf der sich Anbieter 1 in der Kartellsituation befände, bei der beide jeweils 2,5, also jeweils ein Viertel der Sättigungsmenge, anbieten würden. Demzufolge liegt Punkt S senkrecht über der Monopolmenge von 5.
Aus der Abbildung erkennt man noch eine weitere mögliche Ursache für eine Instabilität der Stackelberg-Lösung: Anbieter 1 könnte einen höheren Gewinn realisieren, wenn er seine Menge reduzieren würde. Dann würde er sich nämlich ausgehend von S auf der gepunkteten Linie nach links bewegen. Dort würde er tiefer gelegene Isoprofitkurven erreichen können. Nur sein Wissen, dass Anbieter 2 sofort darauf reagieren würde, hält ihn ab, dieser Versuchung zu folgen.
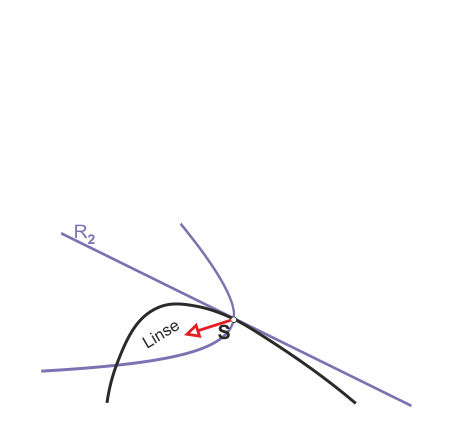
Wenn Anbieter 1 sich in der stärkeren Position wähnt, könnte er Anbieter 2 auch Angebote zum beiderseitigen Vorteil unterbreiten. In S stehen nämlich die Isoprofitkurven der beiden Anbieter senkrecht aufeinander. Wenn Sie das Diagramm anklicken (die entsprechende Isoprofitkurve für Anbieter 2 wird dann eingezeichnet), werden die für dieses Argument wichtigen Kurven angezeigt. Eine Bewegung in Richtung des roten Pfeils in die Linse hinein ließe beide Anbieter auf tiefere Isogewinnkurven kommen, d. h. beide Anbieter könnten gleichzeitig ihren Gewinn erhöhen.