Diese Seite funktioniert nur mit Javascript.
Eindeutigkeit4.1.2.3 StabilitätDas Rentenkonzept

Quelle: Hannoversche Allg. Zeitung, 18.9.98
;
Quelle: Schaumburger Nachrichten, 29.9.05
ragt man nach der Stabilität eines Marktes, dann interessiert man sich dafür, ob ein Markt nach einer Störung wieder ins Gleichgewicht findet. Die Art der Störung spielt dabei eher eine nebensächliche Rolle; z. B. könnte es sich um einen Anstieg der Nachfrage oder um eine Verminderung der Grenzkosten infolge technischen Fortschritts handeln, was eine Zunahme des Angebots zur Folge hätte. Ein solcher exogener Schock wird im Modell durch eine Parameteränderung bei der Angebots- oder Nachfragefunktion abgebildet. Ein Anstieg der Nachfrage würde sich in einer Verlagerung der Nachfragefunktion nach oben ausdrücken, d. h. der Achsenabschnitt $a$ in der (inversen) Nachfragefunktion $p = a - bx$ erhielte einen höheren Wert.
Aus der komparativ statischen Analyse könnte man nun sofort folgern, dass die Konsequenzen dieser Nachfragesteigerung ein steigender Preis und größere gehandelte Menge wären. Bei dieser statischen Betrachtung bleibt aber außer Acht, welchem Pfad Preis und Menge über die Zeit gefolgt sind. In dynamischen mathematischen Modellen, die diese Prozesse mithilfe von Differenzen- oder Differenzialgleichungen abbilden, werden diese Pfade Trajektorien genannt.
Es bleibt noch etwas weiteres verborgen. Es ist nämlich überhaupt nicht sicher, ob die Trajektorie gegen einen festen Endwert strebt, d.h. ob das neue Gleichgewicht überhaupt erreicht wird. Dieser Aspekt verschließt sich der komparativ statischen Analyse.
Um diesen Gedanken zu verdeutlichen, sei folgendes Bild betrachtet: In einem Wald leben Füchse und Hasen. Je mehr Hasen es gibt, desto besser ist die Nahrungsgrundlage für die Füchse und um so schneller vermehren sie sich. Wenn die Fuchspopulation aber wächst, werden mehr Hasen gefressen und der Hasenbestand nimmt ab. Der Hasenbestand beeinflusst also das Wachstum der Fuchspopulation und zugleich beeinflusst der Fuchsbestand das Wachstum der Hasenpopulation.
Nun kann man sich leicht vorstellen, dass in diesem Wald ein Gleichgewicht in dem Sinn existiert, dass die Zahl der Füchse und Hasen über die Zeit konstant ist. Es sind jeweils gerade so viele Füchse und Hasen, dass keine Art die andere in ihrem Bestand gefährdet.
Jetzt sei angenommen, eines Tages wird mitten durch den Wald ein Zaun gezogen, der für Füchse und Hasen unüberwindlich ist. Wenn - was ja recht plausibel ist - das Hase-Fuchs-Problem von den absoluten Beständen unabhängig ist, der Zaun den Wald halbiert und sich auf beiden Seiten des Zaunes je die Hälfte der Füchse und Hasen befindet, so befinden sich die beiden Waldhälften unmittelbar wieder im Gleichgewicht. M.a.W.: gab es ursprünglich ein Gleichgewicht bei 200 Hasen und 20 Füchsen, so gibt es nun in beiden Waldhälften Gleichgewichte mit je 100 Hasen und 10 Füchsen.
Was würde aber passieren, wenn sich bei der Errichtung des Zaunes Hasen und Füchse nicht zu jeweils gleichen Teilen auf die beiden Waldhälften verteilen würden? Würde sich auch dann mit der Zeit in beiden Teilwäldern wieder ein Gleichgewicht einstellen? Wären die Hasen und Füchse in einem der beiden Teilwälder zum Aussterben verdammt? Käme es evtl. zu zyklischen Schwankungen in den Populationen, ohne dass sich die Bestände jemals wieder stabilisieren würden?
Die konkrete Antwort auf diese Frage soll hier gar nicht weiter interessieren (sog. Räuber-Beute-Modelle, das typische Lehrbuchbeispiel für den Einstieg in die Simulation). Im vorliegenden Zusammenhang ist nur folgende Einsicht wichtig: Es ist bekannt, dass nach der Parameteränderung ein Gleichgewicht existiert. Aber es ist nicht gewährleistet, dass es auch erreicht wird. Je nach dem, ob dies der Fall ist oder nicht, wird das System stabil oder instabil genannt. Wird das Gleichgewicht erreicht, so liegt Stabilität vor; wird das Gleichgewicht nicht erreicht, nennt man das System instabil. Mitunter differenziert man noch etwas feiner und spricht von Instabilität, wenn sich das System vom Gleichgewicht weg bewegt, und von einer labilen Situation,
Wie man den Pressemeldungen auf dieser Seite entnehmen kann, lassen sich solche labilen Situationen auf den Märkten für Kartoffeln, Schweine und Informatiker beobachten. Bei Preisen und Mengen kommt es den Beschreibungen nach zu zyklischen Schwankungen. Die Märkte finden nicht in ein stabiles Gleichgewicht.
Es gibt wieder mehr Schlachtschweine
Seitdem massiv weniger Schweine produziert wurden in den Jahren 1995/96 (...), sind die Preise wieder gestiegen. Doch inzwischen zeichnet sich bereits wieder eine Mehrproduktion ab. Laut Monatszahlen des Schweizerischen Bauernverbandes (SBV) lag die produzierte Menge Schweinefleisch im August um 3,5 Prozent höher als im Vergleichsmonat des Vorjahres, im September gar um 10 Prozent höher. «Auch wir sehen, dass die Produktion ansteigt, obwohl wir immer davor gewarnt haben.» Dies betont Adrian Schmitter, Geschäftsführer der Suisseporcs, gegenüber der «BauernZeitung». ... (Hans Rüssli)
Quelle: Bauern-Zeitung, Offizielle Wochenzeitung der bäuerlichen Organisationen der Schweiz, Ausgabe Nr. 47/97 vom 21. November 1997
Cobweb-Modell
In der Folge wird das einfachste und zugleich - wohl gerade auch aus diesem Grund - populärste Modell herangezogen, das solche Prozesse beschreiben kann. Es handelt sich um das Cobweb-Modell oder Spinn(ge)web(s)modell oder -theorem. Mitunter spricht man auch vom Modell des Schweinezyklus, wobei dieser Begriff eigentlich eher für ein ganz spezifisches Resultat des Modells reserviert ist (s.u.). Das Diagramm in Abbildung 3, das entfernt an ein Spinnennetz erinnert, erklärt den Begriff.
Für die Vorstellung des Modells bietet sich der Markt für Ferkel an. Es sei angenommen, im Jahresrhythmus finde eine Auktion statt, auf der die Ferkel versteigert werden. Traditionell - soll heißen, wir sparen uns weitere Erklärungen - werden die Ferkel nur auf der Auktion verkauft, insbesondere gibt es keinen Terminmarkt für Ferkel.
Die Schweinezüchter, die auf diesem Markt als Anbieter auftreten, stehen vor dem Problem, dass sie zum Zeitpunkt der Entscheidung über ihre Angebotsmengen den Preis, zu dem sie verkaufen können, nicht kennen. Die Ferkelzucht dauert halt ihre Zeit (beim Hausschwein beträgt allein die Tragzeit etwa vier Monate).
Woran sollen sich die Anbieter orientieren?
Die mit Abstand häufigste Antwort auf diese Frage lautet: an dem Preis, den sie für ihre Ferkel auf der letzten Auktion erzielt haben. Das sei zum Anlass genommen, zu analysieren, welche Prozesse sich auf diesem Markt abspielen, wenn sich die Züchter bei ihren Produktions- und Angebotsentscheidungen jeweils am Preis der Vorperiode orientieren. Zusätzlich sei noch unterstellt, dass die Regeln der Auktion vorsehen, dass alle zur Auktion angemeldeten Ferkel auch tatsächlich verkauft werden. Ein Züchter hat also nicht die Möglichkeit, Ferkel von der Auktion zurückzuziehen, wenn er mit den Erlösen nicht zufrieden sein sollte.
Zur Nachfrageseite ist wenig zu sagen. Je günstiger die Ferkel zu haben sind, desto mehr werden gekauft; m.a.W.: es gilt das Gesetz der Nachfrage.
Der Ferkelmarkt lässt sich damit wie folgt beschreiben:
$$ {x_t}^A = f(p_{t-1}) \tag{1} $$ $$ {x_t}^N = f(p_{t}) \tag{2} $$Dabei steht ${x_t}^A$ für die Angebotsmenge. Sie ist annahmegemäß abhängig von den Preisen der Vorperiode $p_{t-1}$. ${x_t}^N$ steht für die geplante Nachfrage. Die Nachfrager machen ihre Kaufentscheidung vom aktuellen Preis $p_{t}$ abhängig, der sich auf der Auktion zum Zeitpunkt $t$ herausbildet.
Um das Modell einfach zu halten, werden die Angebots- und Nachfragefunktion wie üblich linear spezifiziert:
$$ {x_t}^A = a + bp_{t-1} \tag{3} $$ $$ {x_t}^N = c + dp_{t} \tag{4} $$Dabei sind $a$, $b$, $c$ und $d$ Parameter, wobei $d$ natürlich negativ zu wählen ist, so dass die Nachfragefunktion fallenden Verlauf zeigt.
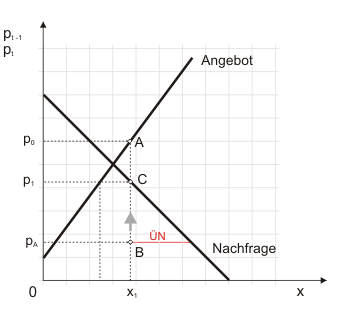
Dieses Modell ist in Abbildung 1 dargestellt. Es unterscheidet sich auf den ersten Blick nicht vom bisher betrachteten Angebots-Nachfrage-Diagramm. Bei genauerer Betrachtung findet man an der Ordinate aber nicht nur den aktuellen, sondern auch den Preis der Vorperiode.
Es sei davon ausgegangen, die Auktion finde in der Region zum ersten Mal statt. Als die Verbandszeitung der Schweinezüchter berichtet, gut unterrichtete Kreise würden mit einem Preis in Höhe von $p_0$ rechnen, verlassen sich die Züchter darauf und planen ein entsprechendes Angebot in Höhe von $x_1$.
Die Angebotsplanung vollzieht sich genau so, wie im Modell der konkurrenzwirtschaftlichen Unternehmung beschrieben. Die Züchter verhalten sich wie Mengenanpasser, die den Preis $p_0$ als Prognose für $p_1$ verwenden und vermuten, dass sie ihn nicht beeinflussen können. Nach der Preis-Grenzkosten-Regel planen sie ihre individuellen Produktionsmengen. Alle zusammen werden die Menge $x_1$ produzieren. Im Unterschied zum bisher betrachteten Modell wird nun aber geraume Zeit vergehen, bis das Angebot auf den Markt kommt. Die Anbieter werden also erst mit erheblicher Verzögerung erfahren, ob ihre Preisvermutung zutrifft.
Mittlerweile sind die Ferkel aufgezogen und der Tag der Auktion ist gekommen. Die Züchter haben $x_1$ Ferkel angemeldet und der markterfahrene Auktionator ruft einen Preis $p_A$ aus, von dem er sicher weiß, dass die Nachfrage das Angebot übersteigt.
Ausgehend von Punkt B kann man in diesem Moment eine Überschussnachfrage ÜN nach Ferkeln erkennen. Da einige Nachfrager offensichtlich bereit sind, höhere Preise zu bezahlen, beginnen sie, sich gegenseitig zu überbieten. Der Preis bewegt sich in Richtung des grauen Pfeils, bis der Auktionator bei einem Preis in Höhe von $p_1$ schließlich den Hammer fallen lässt. Zu diesem Preis sind die Nachfrager gerade bereit, die Menge $x_1$ zu kaufen. Ein höherer Preis hätte sich nur dann eingestellt, wenn das Angebot knapper gewesen wäre.
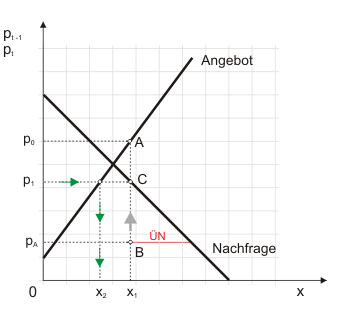
Die Ferkelzüchter sind einigermaßen enttäuscht. Sie hatten mit einem Preis in Höhe von $p_0$ gerechnet, müssen sich aber mit $p_1$ zufrieden geben. Nun kann man sich leicht ausmalen, was passiert, wenn der typische Ferkelzüchter von der Auktion nach Hause kommt und seiner Frau berichtet. Sie wird lamentieren, dass sie ja gleich gesagt habe, die Ferkelzucht lohne kaum noch, und beide werden übereinkommen, in Zukunft weniger Ferkel zu züchten. Die anderen Züchter werden ähnlich reagieren. Der niedrige Preis $p_1$ lässt sie für die zweite Auktion ein Angebot in Höhe von $x_2$ planen (Abbildung 1 zeigt diesen Planungsschritt, wenn Sie die die Grafik anklicken).
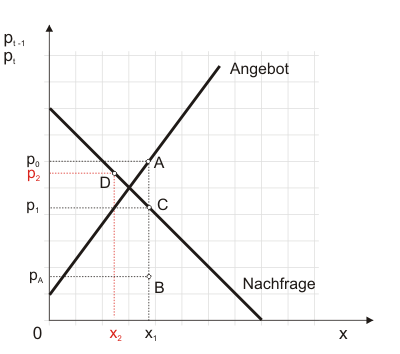
Nun beginnt der Prozess von neuem. Die zweite Auktion rückt näher. Die Züchter bieten die Menge $x_2$ an. Infolge des verknappten Angebots wird mit $p_2$ nun aber ein unerwartet hoher Preis erreicht (Punkt D in Abbildung 2).
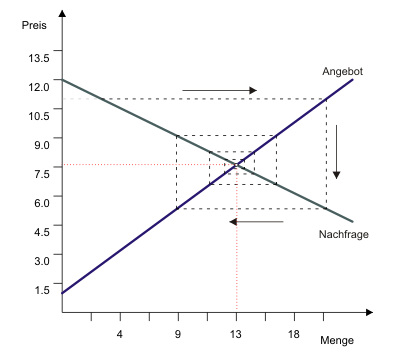
Angebotsfunktion $p_{t-1} = 1 + 0,5x_t^A$
Nachfragefunktion $p_t = 12 - frac{1}{3} x_t^N$
Startpreis $p_0 = 11$
Maßstabsgetreue Darstellung
Nach dieser Auktion schleichen die Züchter nicht wieder mit gesenktem Haupt nach Hause, sondern kehren in die nächste Kneipe ein und feiern erst einmal ihre unerwartet hohen Einnahmen. In ihrer Euphorie planen sie, ihr Angebot für die nächste Auktion auszudehnen. Das wird auf der dritten Auktion die Preise natürlich drücken ... und es ist leicht einzusehen, dass das Verhalten der Züchter dazu führt, dass Erfolge und Misserfolge sich abwechseln.
Wenn man die Maus über Abb. 2 stellt, kann man die Mengen-Preis-Kombinationen in den drei folgenden Perioden ablesen. Abb. 3 zeigt maßstabsgetreu ein konkretes Zahlenbeispiel.
In den beiden in Abbildungen 2 und 3 dargestellten Fällen kann man erkennen, wie sich der Preis dem Gleichgewichtspreis immer mehr annähert. Die Märkte sind demnach stabil, denn sie finden ins Gleichgewicht (mal abgesehen davon, dass der Prozess theoretisch unendlich lange dauern würde).
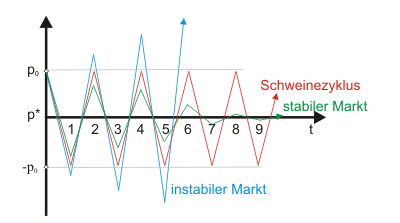
Dieser Fall muss aber nicht eintreten. Auch ohne eine analytische Lösung des Problems (etwas anspruchsvoller) zu betrachten, kann man aus der grafischen Darstellung leicht erkennen, dass man sich immerwährend im Kreis drehen würde, wenn Angebots- und Nachfragefunktion die (absolut) gleiche Steigung besäßen. Von Periode zu Periode läge der Preis immer um den gleichen Betrag einmal über und einmal unter dem Gleichgewichtspreis. Diese fortwährende Schwankung um den Gleichgewichtspreis mit konstanter Amplitude bezeichnet man als Schweinezyklus (im engeren Sinne).
Denkbar ist natürlich ebenfalls, dass sich der Preis immer weiter vom Gleichgewichtspreis entfernt. Dieser Fall des instabilen Marktes würde eintreten, wenn die Angebotsfunktion "flacher" verliefe als die Nachfragefunktion. Eigentlich sollte man natürlich eleganter formulieren: ... wenn das Angebot elastischer auf den Preis reagiert als die Nachfrage.
Dass in den Abbildungen 2 und 3 stabile Märkte zu beobachten sind, liegt an dem relativ - im Vergleich zur Nachfrage - unelastischen Angebot. Hier reagieren die Anbieter auf die Preisschwankungen vergleichsweise moderat, wodurch die Preisschwankungen gedämpft werden. Das ist auch intuitiv plausibel, denn die Märkte werden natürlich um so eher zur Instabilität neigen, je elastischer das Angebot auf Preisschwankungen reagiert.
Abbildung 4 zeigt schematisch die drei denkbaren Preisentwicklungen über die Zeit.
Wie viel Informatiker braucht das Land?
Mitte der 90er Jahre wollte kaum jemand Informatik studieren. Heute werden IT-Experten händeringend gesucht. Die Zahl der Studienanfänger explodiert.
... 'Leider lassen sich die Abiturienten stark vom aktuellen Arbeitsmarkt beeindrucken', kommentiert Stefan Pfisterer von Bitkom die Entwicklung. Nur wenige Studenten würden antizyklisch studieren. ... Das könne sich demnächst ändern. Ende der 90er Jahre explodierte die Zahl der Studienanfänger im Fach Informatik regelrecht. Im Jahr 2000 haben sich 38000 Studenten eingeschrieben, fast dreimal so viele wie 1995. Droht hier ein neuer Schweinezyklus? (Holger Dambeck, aus c\'t 2001, Heft 5, 66).
- Welches Gut wird hier produziert? Ist das Produkt "lagerfähig"? Wie lange dauert die Produktion in der Regel? Wer sind Anbieter und wer sind Nachfrager auf diesem Markt? Warum könnte ein Schweinezyklus drohen? Welche anderen Märkte haben ähnliche Eigenschaften?
Eine häufige Frage (oder Kritik) bezieht sich auf den instabilen Markt. Eine solche Entwicklung könnte doch gar nicht denkbar sein, da Preise und Mengen hier nach einigen Perioden negative Werte annehmen. Nun, zunächst einmal erklärt das Modell, dass sich der Preis vom Gleichgewichtspreis entfernen kann. Dass dieser Prozess nicht zum Stillstand kommt, liegt einfach an der simplen Konstruktion des Modells, in dem die Anbieter den gegenwärtigen Preis immer für die beste Prognose für den zukünftigen Preis halten. Obwohl sie wieder und wieder mit ihrer Prognose Schiffbruch erleiden, halten sie dennoch an ihrem Verfahren fest.
Diese Modellannahme wird der Realität natürlich nicht gerecht. Die Anbieter werden wahrscheinlich aus Erfahrung klug und erkennen, dass sie sich antizyklisch verhalten müssen, wenn sie ihren Gewinn maximieren wollen. Gewinnen einige Anbieter diesen Durchblick, würden sie gerade dann ihre Produktion ausdehnen, wenn der gegenwärtige Preis niedrig ist, und somit zu einer Stabilisierung des Marktes beitragen. Problematisch wäre natürlich der extreme Fall, dass alle Anbieter zugleich ihr Verhalten ändern würden.
Im Zusammenhang mit der Stabilität von Märkten tauchen oft die Begriffe Walras- und Marshall-stabil auf. Um mehr darüber zu erfahren, folgen Sie diesem Link.
Ein weiterer kritischer Einwand setzt an der Annahme an, dass die Anbieter ihre Produktion auf jeden Fall verkaufen. Zahlreiche Produkte sind aber lagerfähig. Bei niedrigen Preisen könnten die Anbieter Lager auf- und bei hohen Preisen Lagerbestände abbauen. Auch das würde den Markt stabilisieren (helfen).
Andererseits kann man - die Beispiele auf dieser Seite deuten zumindest in diese Richtung - durchaus Märkte beobachten, auf denen es zu regelmäßigen Preisschwankungen kommt. Und die Gründe, die dafür vermutet werden, sind jeweils jene, die die beiden zentralen Annahmen im Cobweb-Modell bilden: (a) die Anbieter lassen sich in ihren Produktionsentscheidungen vor allem von der gegenwärtigen Marktlage leiten und (b) die Produktion des Gutes erfordert geraume Zeit.
Nach ähnlichen Seiten im WWW suchen