Diese Seite funktioniert nur mit Javascript.
Durchschnitts- und Grenzprodukt3.2.4 Substitutionale Produktionsfunktionen, IsoquantenGrenzrate der technischen Substitution
ieser Abschnitt stellt mit einer limitationalen Produktionsfunktion das genaue Gegenteil von dem an den Anfang, was seiner Überschrift nach zu erwarten wäre. Abbildung 1 zeigt einen Prozessstrahl für einen Produktionsprozess, von dem Folgendes angenommen sei: Mit Hilfe von Kapital $K$ und Arbeit $L$ wird ein Produkt X erzeugt, dessen Menge mit $x$. Technologisch bedingt müssen Kapital und Arbeit im Verhältnis 1:2 eingesetzt werden. Zur Produktion je einer Einheit X sind 2 Einheiten Kapital und 4 Einheiten Arbeit notwendig.
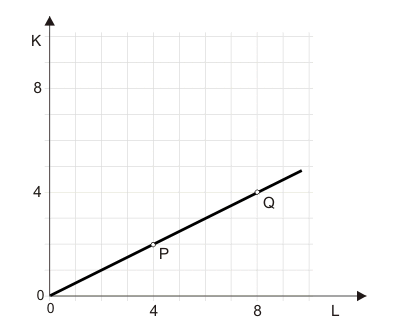
Punkt P in der Abbildung zeigt die Produktion von einem X, Punkt Q entspricht der Produktion von zwei X. Dass nicht nur die beiden Punkte dargestellt sind, sondern eine durchgehende Linie eingezeichnet ist, zeigt an, dass auch nicht ganzzahlige Mengen von $x$ herstellbar sind (R in Abbildung 2 zeigt die Produktionsmenge $x = 1,5$).
Der Faktor limitiert die Produktion. Formal kann man eine limitationale Produktionsfunktion angeben als
$$ x = min \Bigl(\cfrac{K}{a},\cfrac{L}{b} \Bigr) \tag{1} $$Wenn Sie den Operator $\text{min}$ nicht kennen, verwenden Sie den
mit den Parametern $a$ und $b$, die Inputkoeffizienten heißen. Diese geben an, welche Menge eines Faktors je Produkteinheit bei effizienter Produktion erforderlich ist. Im Beispiel ist der Inputkoeffizient $a$ des Kapitals 2 und der Inputkoeffizient $b$ der Arbeit 4. Wenn 8 Einheiten Kapital und 8 Einheiten Arbeit zur Verfügung stünden, ließen sich 2 Einheiten X herstellen. Arbeit wäre in diesem Fall der limitierende Faktor, 4 Einheiten Kapital kämen nicht zum Einsatz.
Auf diesen Aspekt geht der Abschnitt Skalenerträge näher ein. Die Limitationalität der Produktionsfaktoren bewirkt, dass ihr Einsatzverhältnis nicht von den Faktorpreisen abhängt (ein Kfz benötigt eine Windschutzscheibe - wenn diese günstiger oder teurer werden, werden deswegen nicht mehr oder weniger davon eingebaut). Leontief-Produktionsfunktionen kommen in den Wirtschaftswissenschaften recht häufig zum Einsatz, da sie infolge ihrer Linearität mit Hilfe der Matrixalgebra einfach zu handhaben sind (z.B. in der die Volkswirtschaftliche Gesamtrechnung unterstützenden Input-Output-Rechnung oder bei der Produktionsprogrammplanung, um auch ein Beispiel aus der Betriebswirtschaftslehre zu nennen).
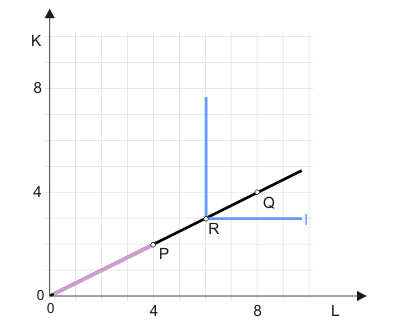
In Abbildung 2 ist mit dem durch Punkt R gekennzeichneten Faktoreinsatz die Produktion von 1,5 Einheiten X möglich. Die blaue in R rechtwinklig abknickende Kurve I zeigt weitere Kombinationen der Faktoren, mit denen 1,5 Mengeneinheiten X hergestellt werden könnten. Bis auf die Kombination R sind aber alle Faktorkombinationen auf dieser Isoquante ineffizient. Im waagerechten Teil ist Kapital der limitierende Faktor, im senkrechten Teil Arbeit.
Die Isoquante in Abbildung 2 schrumpft also eigentlich auf den Punkt R zusammen - es ist (im vorliegenden Fall einer limitationalen Produktionsfunktion) jedoch anschaulicher, auch die ineffizienten Bereiche anzuzeigen. Natürlich könnte man auch für die Punkte P oder Q oder für jeden beliebigen anderen Punkt eine Isoquante einzeichnen. Wie Indifferenzkurven in der Haushaltstheorie füllen sie das gesamte Diagramm aus, zeigen aber im Unterschied zu diesen mit der Produktionsmenge eine beobacht- und messbare Größe.
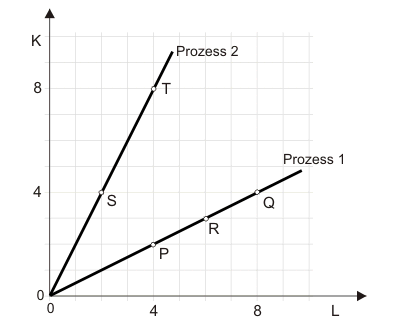
In Abbildung 3 ist angenommen, dass ein zweiter Prozess für die Produktion des Gutes X existiert, der als Prozess 2 eingezeichnet ist. Er kann beschrieben werden durch
$$ x = min \Bigl(\cfrac{K}{4},\cfrac{L}{2} \Bigr) \tag{2} $$Die eingezeichneten Punkte S und T zeigen also die Produktionsmengen $x=1$ bzw. $x=2$ an.
Wenn zwei Prozesse existieren, verschwindet die Limitationalität, denn es ist jetzt z.B. möglich, Kapital und Arbeit im Verhältnis 1:1 zu beschäftigen. Abbildung 4 zeigt, wie 2 X bei diesem Faktoreinsatzverhältnis hergestellt werden können. 1 X wird im Prozess 1 und 1 X im Prozess zwei hergestellt, sodass insgesamt 6 Einheiten Arbeit und 6 Einheiten Kapital eingesetzt werden.
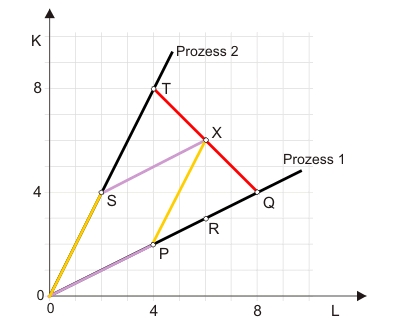
Wie man aus dem Parallelogramm in Abbildung 4 erkennt, liegt der Punkt X, der die Produktionsmenge 2 anzeigt, auf der Verbindungsgeraden der beiden Punkte T und Q, die in den Prozessen 1 und 2 jeweils die Produktionsmenge 2 anzeigen. Alle Punkte auf dieser Verbindungsgeraden zeigen Kombinationen der beiden Prozesse, die zu dem gleichen Produktionsergebnis von 2 X führen. Abbildung 5 zeigt ein Beispiel, in dem Prozess 1 relativ intensiv genutzt wird: 0,5 X werden mit Prozess 2 und 1,5 X mit Prozess 1 hergestellt.
Da die Produktionsmenge auf der roten Verbindungsgerade konstant ist, handelt es sich bei ihr um eine Isoquante. Wenn man sich auf ihr vom Punkt T hin zum Punkt Q bewegt, ändert sich die Kapitalintensität der Produktion - das Einsatzverhältnis von Kapital und Arbeit $k=K/L$ - von $k=2$ auf $k=1/2$. Bei gleicher Produktionshöhe wird also Kapital gegen Arbeit substituiert. TQ zeigt somit eine Isoquante für eine begrenzt substitutionale Produktion; begrenzt deswegen, weil die beiden Faktoren nicht vollkommen gegeneinander substituiert werden können.
Es bietet sich an, anhand Abbildung 5 zu überlegen, unter welchen Umständen sich ein Produzent für Prozess 1, Prozess 2 oder eine Kombination von beiden entscheiden würde. Angenommen eine Einheit Kapital ist teurer als eine Einheit Arbeit, dann wäre Prozess 1 offenbar am günstigsten. Umgekehrt, also wenn Arbeit teurer wäre, würde der kapitalintensive Prozess 2 gewählt. Nur wenn beide Faktoren je Einheit gleich teuer wären, kämen alle Prozesse gleichermaßen in Frage.
Andere Produktionsfunktionen zeigen andere Isoquantenverläufe. Eine der bekanntesten und in der Mikro- wie Makroökonomie (und auch in der betriebswirtschaftlichen Produktionstheorie) sehr häufig verwandte Produktionsfunktion ist die nach Cobb und Douglas benannte Cobb-Douglas-Produktionsfunktion (deren Funktionstyp auch oft - so wie hier geschehen - aufgrund ihrer einfachen Handhabbarkeit als Nutzenfunktion in der Haushaltstheorie zum Einsatz kommt), die sie zwar nicht "erfunden", aber populär gemacht haben. Die Cobb-Douglas-Funktion hat die allgemeine Form
$$ x = c K^a L^b \tag{3} $$Dabei ist $c$ ein Effizienzparameter, der aber verzichtbar ist, da man $x$ entsprechend normieren kann. Die Funktion besitzt die hübsche Eigenschaft, dass die Parameter $a$ und $b$ mit den partiellen Produktionselastizitäten des Kapitals und der Arbeit übereinstimmen.
$$ E_{x,L} = \cfrac{\partial x}{\partial L} \cfrac{L}{x} = bcK^aL^{b-1} \cfrac{L}{c K^a L^b} = b \tag{4} $$Die Produktionsfunktion laute $ x = K^{0.5} L^{0.5} $.
Berechnen Sie, wie viel $x$ Sie mit fünf Einheiten Kapital und 20 Einheiten Arbeit erzeugen können.Wenn Sie es nicht im Kopf lösen können, verwenden Sie den Rechner und geben Sie 5^0.5*20^0.5 ein.
In Abbildung 6 ist die Produktionsfunktion am Zahlenbeispiel $ x = K^{0.5} L^{0.5} $ dargestellt. Wenn je 10 Einheiten Kapital und Arbeit eingesetzt werden, werden 10 Einheiten X hergestellt. Die Isoquante für diese Produktionsmenge ist hervorgehoben. Die Abbildung zeigt, dass es sich bei den Isoquanten um "Isohöhenlinien des Produktionsgebirges" handelt. Der vorn in der Abbildung grün zu erkennende Schnitt durch das Produktionsgebirge zeigt eine Ertragskurve bei partieller Faktorvariation für einen bei $K=20$ konstant gehaltenen Kapitaleinsatz.
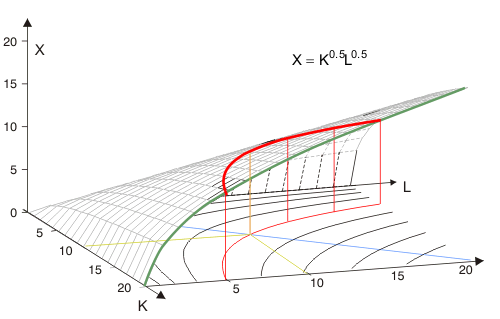
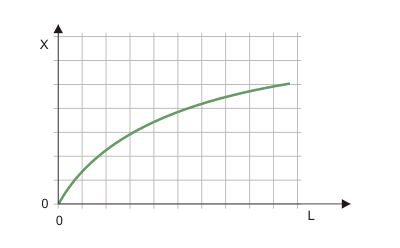
Abbildung 7 zeigt diese Ertragskurve bei partieller Faktorvariation (im Unterschied zu Abbildung 6 nicht mehr maßstabsgetreu). Man erkennt in ihr die Eigenschaften einer neoklassischen Produktionsfunktion. Die Grenzerträge sind positiv und abnehmend. Die partielle Produktionselastizität liegt unter 1.
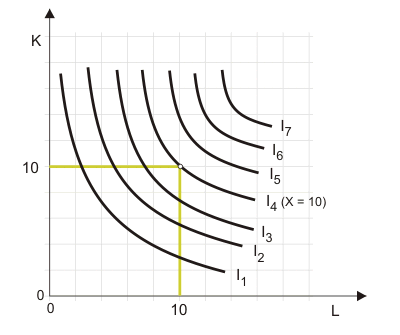
Abbildung 8 zeigt das Produktionsgebirge "aus der Vogelperspektive". Die "Isohöhenlinien" erscheinen als Isoquanten.
Nach ähnlichen Seiten im WWW suchen